8.2.3 冯氏明暗绘制方法
��冯氏（Phong）明暗处理方法的基本思想是：多边形内各点的法向量通过对顶点的法向量作双线性插值得到，在多边形内构造一个连续变化的法向量函数，并将它代入光亮度计算公式，即得到由多边形近似表示的曲面在各采样点处的光亮度值。因此，冯氏明暗处理方法又叫法向量插值明暗处理方法。它能够更真实地表现物体表面的高光效果，并缓解马赫带效应。但是由于每一个象素点的光亮度值都需要进行光照模型计算，故计算量较大。
��冯氏明暗处理的一般步骤：
��1) 计算每个多边形顶点的平均单位法矢量；
��2) 对多边形顶点的法矢量进行双线性插值，得到多边形内每个点的法矢量；
��3) 根据光照模型沿每条扫描线计算多边形内各点对应的投影象素的光强度值。
��对于多边形内任意一点的法矢量的双线性插值的计算公式与高若德明暗绘制方法中的类似，只不过是把其中的光强项用法向量项来代替罢了，在这里我们沿用图8.5的记号，并把I换为N，则P点处的法矢量NP就有如下的插值公式：

N5=uN1+(1-u)N2, u=(Y5-Y2)/(Y1-Y2)；

N6=vN1+(1-v)N4, v=( Y6-Y4 )/(Y1-Y4)；

NP=tN5+(1-t)N5, t=(Xp-X6)/(X5- X6)。
��同时，两条相邻的扫描线与同一条边的交点的法向量的增量插值计算的公式也与光强插值公式相似，我们只要用法向量代替光强即可：
��如图8.6所示，设Y坐标分别为y和y-1的两条扫描线与多边形的边V1V2的交点的法向量分别为N5和N，则
。

但是，当多边形为三角形时，插值公式更简单。
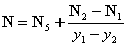��设屏幕坐标系为xoy，如图8.7所示，P1、P2和P3是三角形三个顶点在屏幕上的投影坐标。建立三角形仿射坐标系 ，其中P1、P2和P3的仿射坐标为(0,0)，(1,0)和(0,1)，从屏幕坐标到三角形仿射坐标的变换为：