8.1.3 镜面反射光和冯(Phong)氏反射模型
��当我们观察一个光照下的光滑表面，特别是有光泽的表面时，可能在某个方向上看到很强的高光，这个现象称为镜面反射。
��在正常情况下，光沿着直线传播，当光遇到不同的介质表面时，会产生反射和折射现象，而且在反射和折射的时候，它们遵循反射定律和折射定律：
��（1） 反射定律
��（2） 折射定律
��一般来说，从物体表面反射或折射出来的光的强度取决于光源的位置与光的强度、物体表面的位置和朝向、表面材质的性质和视点的位置。对于理想镜面，反射光都将集中在镜面的反射方向上，视线只有在与反射光线重合时才能观察到镜面反射光。但是，对于那些非理想的镜面，由于表面实际上是由许多不同朝向的微小平面组成，镜面反射光将分布于表面的镜面反射方向的周围。在实际应用时，常常作适当的简化。冯（Phong）提出了一个计算镜面反射光亮度的经验模型，其计算公式为：
（8－1－3）
，
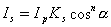其中：Ks是物体表面镜面反射系数，它与入射角和波长有关；α是视线与反射方向的夹角；n为镜面高光系数，用来模拟镜面反射光在空间中的汇聚程度，它是一个反映物体表面光泽度的常数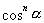； 近似地描述了镜面反射光的空间分布。
��令V和R分别是观察方向和镜面反射方向的单位矢量，则我们可以用点积V・R来代替 ：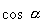
（8－1－4）

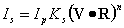
其中，矢量R可以通过入射光单位矢量L和单位法矢量N计算出来：在图8.3中，我们有
�R ＋ L ＝ （2cosθ ）N
�����= 2（N・L）N，
所以，
��R ＝ 2（N・L）N－L。
在多个点光源照射下，冯氏镜面反射模型可以写成：
，
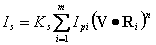其中，m是光源的个数，Ri是相对于第i个光源的镜面反射方向，Ipi是第i个光源的光强。
��引入矢量L和V的半角矢量H（见图8.3），上述镜面反射的经验模型还可以进一步进行简化，得到简化的冯模型： 用（N・H）代替（8－1－4）式中的（V・R）、用cosβ代替cosα，即
（8－1－5）

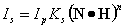
其中， 。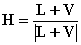
��在多个点光源照射下，简化的冯模型为：

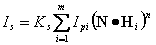
其中Hi是第i个光源的入射光单位矢量Li和视方向矢量V的半角矢量。