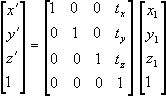
已知变量 v(t)的两个值，t=0和t=1时，v1=v(0)，v2=v(1)则两个值的线性插值为 　　　　　v(t)=(1-t)v1+tv2　对 0≤t≤1 　　例如已知两个点，t=0时，P1(x1,y1,z1)，t=1时，P2(x2,y2,z2)， 则t=t时，点P(x,y,z)(相当于物体均速运动) 　　　　x(t)=(1-t)x1+tx2 　　　　y(t)=(1-t)y1+ty2 　　　　z(t)=(1-t)z1+tz2 　　设物体上一个点的两个位置，t=0时P1(x1,y1,z1)，t=1时P2(x2,y2,z2)，则该物体上这一个点的位置，t=t时，P'(x',y',z')。 　　　　 　　其中： tx=(x2-x1)t 　　　　　 ty=(y2-y1)t 　　　　　 tz=(z2-z1)t 　　线性插值是把各中间点，按照与自变量的线性关系，均匀分布。如果把自变量理解为时间量，这相当于沿着直线以匀速运动，通过各中间点。