2.非线性插值:
实际物体运动有时不是匀速的,从零初速度加速,再减速,并停止在终点。这时用非线性插值。可以把上述计算公式改变如下。
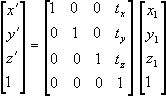
其中 tx=(x2-x1)f
ty=(y2-y1)f
tz=(z2-z1)f
f=0.5・(1+cosθ)
θ=(1-t)π+t・2π
当t=0→1时,θ=π→2π,θ对t成线性关系
f=0→1,f对t成非线性关系(三角函数)
| 4.4.1 插值方法 2.非线性插值: 实际物体运动有时不是匀速的,从零初速度加速,再减速,并停止在终点。这时用非线性插值。可以把上述计算公式改变如下。 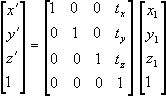 其中 tx=(x2-x1)f ty=(y2-y1)f tz=(z2-z1)f f=0.5・(1+cosθ) θ=(1-t)π+t・2π 当t=0→1时,θ=π→2π,θ对t成线性关系 f=0→1,f对t成非线性关系(三角函数) |