求监督码元多项式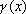 的过程由下式确定, 的过程由下式确定,
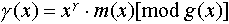 (3-15) (3-15)
其中,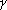 为监督位的位数。上式的含义是可以用信息码元多项式m(x)乘 为监督位的位数。上式的含义是可以用信息码元多项式m(x)乘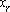 ,然后用g(x)除,就求得余式 ,然后用g(x)除,就求得余式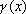 ,即为监督位多项式 ,即为监督位多项式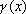 。由 。由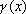 可求得监督位 可求得监督位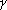 。由此可以求得编码后得到的码字多项式为: 。由此可以求得编码后得到的码字多项式为:
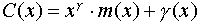 (3-16) (3-16)
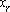 乘m(x)相当于将信息码字左移 乘m(x)相当于将信息码字左移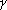 位,若m=[1010], 位,若m=[1010],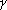 =3,令m3= =3,令m3=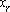 m(x),则m3=[1010000]。右边的3位可用于加上监督码元 m(x),则m3=[1010000]。右边的3位可用于加上监督码元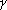 。这种信息码元在前,监督码元在后的形式一股称为系统码。
。这种信息码元在前,监督码元在后的形式一股称为系统码。
由于在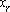 ・m(x)的基础上加上 ・m(x)的基础上加上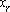 m(x)/g(x)的余式 m(x)/g(x)的余式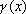 ,显然c(x)应该能被g(x)整除。收端利用此性质可以判定收码多项式R(x)的正确性,若传输过程中无错码,有R(x)=C(x),R(x)能被整除。若R(x)有错码,则R(x)=c(x)+E(x),E(x)可称为错误图样多项式。由E(x)可定义校正子多项式,常称为伴随式S(x)=E(x)/g(x)。在纠错能力范围内,S(x)和E(x)有一一对应的关系。利用下式可实现纠错, ,显然c(x)应该能被g(x)整除。收端利用此性质可以判定收码多项式R(x)的正确性,若传输过程中无错码,有R(x)=C(x),R(x)能被整除。若R(x)有错码,则R(x)=c(x)+E(x),E(x)可称为错误图样多项式。由E(x)可定义校正子多项式,常称为伴随式S(x)=E(x)/g(x)。在纠错能力范围内,S(x)和E(x)有一一对应的关系。利用下式可实现纠错,
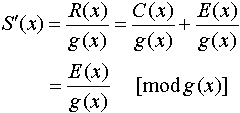 (3-17) (3-17)
求得S'(x)以后与S(x)比较,可确定E(x),并进行纠错。
|
|
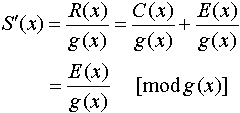 (3-17)
(3-17)