(1) 连续信道的信道容量
根据香农(shannon)定律,在高斯白噪声干扰下的信道中,信道容量:
C=Blg(1+S/N) (b/s)
式中:B--信道带宽; S--信号功率; N--白噪声功率。
白噪声是指在所有频率上噪声强度都一样,就像白光所包含的各种频率的光波基本上都一样强那样;而且服从高斯型的概率分布。这就是小幅度的噪声出现的概率较大,大幅度噪声出现的概率急剧下降。
(2) 离散信道的信道容量
根据取样定理,可以得到无噪声的信道容量,这是因为已把信道的带宽与信道上传送的最大符号率建立了关系。在只有两个离散值的二元信道中,即一个符号以1比特发送,那么信道就能发送2Bb/s。当符号具有L个离散值时,无噪声信道容量:
C=2Blog2L(b/s)
在有噪声的情况下,要造成传输差错,损失信息和降低信道容量。以二元信道为例,通过理论计算,得出信道收到的一个符号的信息量最大值是:
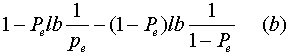
其中:Pe--发生差错的概率
上式计算的条件是原发符号中出现"1"和"0"的概率都是1/2,后面二项是信号损失,因此这种二元信道的信道容量:
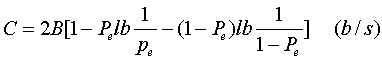
若假设Pe=0.1则由上式算出C=0.53(2B),这说明一个二进制符号只能传输0.53b的信息,使有效的信息速率降低一半。
|