对于一个非周期信号f(t)，我们可构造一个新的周期信号fT0(t)，即由f(t)每隔T0重复，若周期T0选得足够长，以致于使得重复脉冲信号之间不产生重叠，这一延拓了的周期信号fT0(t)和原信号f(t)之间的关系为 　　　 　　该周期函数fT0(t)可用博氏级数来表示，即 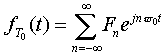　　　 　　现在我们来考察当T0∞时频谱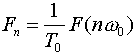变化的特点，我们定义w的连续函数F(w)， 　　　 　　可看出， 　　　 　　因此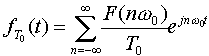， 　　　 　　用Δω代表ω0，则当T0趋于无穷大时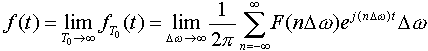， 　 　　上式可进一步变为 　　　 　　此式称为傅氏积分，它们的意义是任意一个非周期信号可以表示为加权了的虚指数分量ejwt之和，而不是用傅氏级数来表示，这一加权值为F(w)dw/2π，而F(w)通常称为频谱密度函数(沿w的长度分布)。 　　通常，我们称F(w)为f(t)的正变换，f(t)为F(w)的反变换，它也用下列符号表示为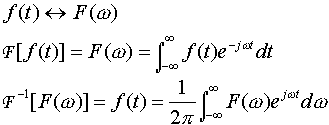：