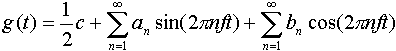(3-1) 　　此处f＝1/T是基频，an和bn是正弦和余弦函数的n次谐波（Harmonics）的振幅。这种分解叫做傅立叶级数（fourier series）。通过傅立叶级数可以重新合成原始函数，即，已知周期T和振幅，通过(3-1)求和能够得到时间函数g(t)。 　　可以把一个持续时间有限的数据信号（所有的信号都是如此），想象成它在一遍又一遍地无限重复整个模式（即区间T到2T的模式等同于区间0到T，依此类推）。 　　对任何给定的g(t)，通过对(3-1)式两边同乘sin(2πkft)，然后从0到T积分，可得到振幅an，因为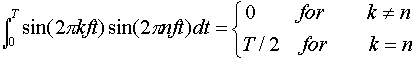： 　　 　　和式中只留下an，bn消失。类似地，用cos(2πkft)乘(3-1)式两边，然后从0到T积分，可得bn。另外，直接对(3-1)式两边积分，即可得c。执行这些运算的结果如下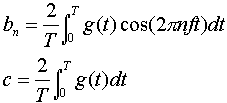： 　　　 　　　 　　由于正弦量可以写成两个虚指数分量之和，所以傅立叶级数可以表示成指数型级数的形式。 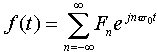　　　 　　其中，F0=c/2，Fn=1/2( an-jbn )，F-n=1/2( an+jbn )，w0=2π/T0 。 　　根据上面的an，bn的计算式，可得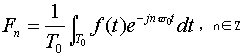，