1.基本模型

　　假设有一个包含M个任务的应用程序，我们希望在一个由N台处理机组成的系统上以最快的速度执行这个程序。为了简单起见，我们先考虑一个仅有两台处理机的系统，然后再逐步增加处理机数目。为了模拟性能，我们需要用公式表示出执行时间和额外开销。
　　我们先承认下面两个假设是成立的，以获得初步结论，然后放宽假设，观察性能如何变化。
　　1.每个任务的执行时间为R个单位。
　　2.当两个任务不在同一台处理机上时，其通信所需的额外开销为C个单位时间。当两个任务在同一台处理机上时，通信所需的额外开销为0。
　　一个应用程序在两台处理机系统上运行有多种分配方法。我们可以把全部任务都分配给一台处理机而另一台空闲，这种分配方法的通信开销最小，但没有利用并行性。我们也可以按各种不同比例将任务分配给两台处理机，那么总处理时间是执行时间和额外开销时间之和。我们用C表示用于通信的时间，其实它还包括系统所有其它额外开销。
　　在某些情况下，系统的额外开销的操作可以与计算过程重叠进行，例如处理机在执行指令的同时能通过Ｉ／Ｏ接口进行通信。当然并不是所有的额外开销都可以被屏蔽掉，例如处理机在访问共享数据或通信通路时可能会发生竞争，处理机在等待同步信号期间处于空闲状态等。因此，我们假设一部分额外开销的操作会增加总处理时间。在这种情况下，可以用下列等式表示一个程序的总处理时间：
　　总处理时间＝RMａｘ（M－K，K）＋C（M－K）K （8.1）
　　等式（8.1）表示总处理时间是两个时间的和，一个是执行时间，另一个是用于通信和其它额外开销的时间。对两台处理机系统来说，执行时间取两台处理机执行时间较大的一个。因此当K个任务分配给一台处理机，剩下的（M－K）个任务分配给另一台处理机时，执行时间取R（M－K）和RK中较大的一个。我们称K为任务分配参数。第二项表示额外开销时间与通信次数成正比例关系。通信次数与任务分配方法有关。从（8.1）式可知，第一项是K的线性函数，第二项是K的二次函数。
　　从等式（8.1）可知总处理时间是K的函数，那么其最小值是多少呢？也就是说，任务如何分配才能获得最小的总处理时间？我们可以采用如图8.11所示的图解法来求最小处理时间。

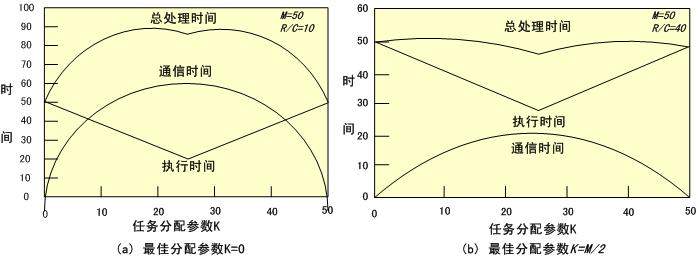
图8.11 两种不同R/C比值的并行执行时间

　　对于该模型的结论是：当R/C＜M/2时，把所有任务分配给同一台处理机能使总处理时间最小；当R/C＞M/2时，把任务平均地分配给两台处理机能使总处理时间最小。也就是说使任务分配参数K＝0或K＝M/2。当M为奇数时，应使K尽可能接近M/2。图8.11的横坐标是任务分配参数K，纵坐标是总处理时间。图8.11（ａ）和（ｂ）分别表示R/C小于M/2和R/C大于M/2时任务分配参数K与总处理时间的关系。等式（8.1）的第一项执行时间是分段线性的，在图8.11中这一项看起来好象字母Ｖ，它对称于K＝M/2。图8.11（ａ）中，由于二次曲线K（M－K）的开口朝下，叠加一个线性项后开口仍朝下，所以最小值一定在区间0≤K≤M/2的端点处，即K＝0（或K＝M）时为最小值。图8.11（ｂ）中，当分段线性项与二次函数项叠加后，在K＝M/2处为最小值。