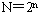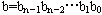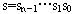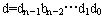＊超立方体网络的E立方体寻径 假设有一个结点的n方体。每个结点的二进制编码为。这样，源结点为，目的结点。现在要确定一条从s到d的步数最小的路径。
　　将n维表示成i=1,2,…n，其中第i维对应于结点地址中的第i-1位。设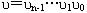是路径中的任一结点。路径可以根据以下方法唯一地确定。
　　1.计算方向位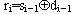，其中i=1,2,…,n。
　　使i=1,u=s，开始以下步骤。
　　2.如果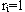，则从当前结点u寻径到下一结点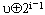。如果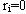，则跳过这一步。
　　3.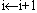。如果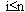，则转第2步，否则退出。
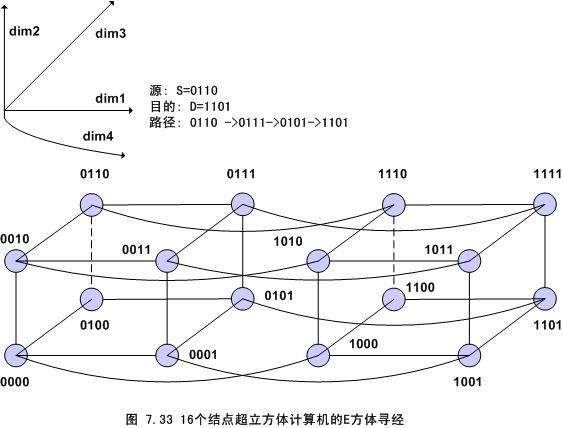
　　下面用图7.33中的例子来说明上述E方体寻径算法。例中，n=4,s=0110,d=1101,因此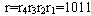。由于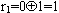,因此s就寻径到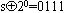。由于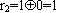,因此u＝0111就寻径到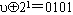。由于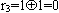,因此就可跳过维i=3这一步。由于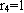,因此u＝0101就寻径到。
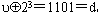　　所选择的路径在图7.33中用箭头所示。注意，寻径是按照从维1到维4的顺序进行的。如果s和d的第i位相同，则沿维i方向不需要寻径，否则从当前结点沿着这一维方向走到其它结点，重复这一过程直到到达目的结点。
　　E立方体寻径也不会产生死锁寻径，也可用于存储转发和虫蚀网络，在源和结点之间形成一条距离最短的路径。