（8）超立方体 这是一种二元n-立方体结构，它已在iPSC、nCUBE和CM-2系统中得到实现。一般说来，一个n-立方体由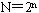个结点组成，它们分布在n维上，每维有两个结点。8个结点的3-立方体如图7.16a所示。
　　4-立方体可通过将两个3-立方体的相应结点互连组成。如图7.16b所示。一个n-立方体的结点度等于n，也就是网格的直径。实际上，结点度随维数线性地增加，所以很难设想超立方体是一种可扩展结构。
　　在80年代的研究开发工作中，二元超立方体是一种极为普遍采用的结构。Intel iPSC/1、iPSC/2和nCUBE机都是用超立方体结构制造的，这种结构的连接比较密集。许多其它结构诸如二叉树、网格形等都能嵌入超立方体。
　　由于缺乏可扩展性以及难于组成高维超立方体，所以超立方体结构正逐渐被其它结构所取代。例如，CM-5选用了胜过CM-2超立方体的胖树形结构。Intel Paragon选用了较其前身超立方体更好的2维网格形结构。拓扑等效已在许多网络结构之间得到证实。一种结构能在未来的系统中继续生存下去的基础是它能够模块地增长，以便高效组装起来，具备可扩展性。

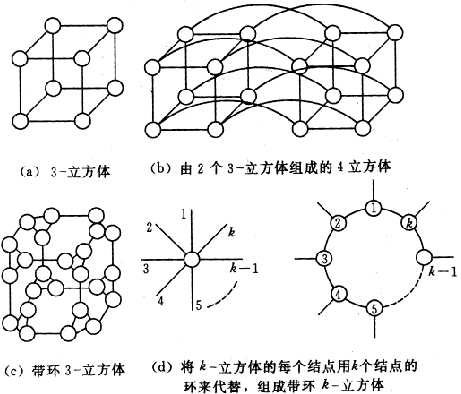
图7.16 超立方体和带环立方体

　　（9）带环立方体 这种结构是从超立方体改进而来的。如图7.16c所示，一个3-立方体可改成带环3-立方体（CCC）。构成的办法是将3-立方体的角结点（顶角）用一个结点环来代替。
　　一般说来，我们可以从一个k-立方体构成一个有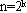个结点环的带环k-立方体，如图7.16d所示。所用的办法是用k个结点的环取代k维超立方体的每个顶角。这样，一个k-立方体可变成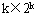个结点的k-CCC。
　　图7.16c所示3-CCC的直径为6，比原来3-立方体的直径大一倍。一般说来，k-CCC的网格直径2k。CCC的主要改进之处即在其结点度为常数3，与超立方体的维数无关。
　　假设一超立方体有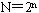结点。一个有同样N结点数的CCC一定是由低维k-立方体组成，即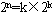，其中k<n。
　　例如，对应于n=6和k=4的情况，一个64结点的CCC可用4结点的环取代4-立方体的角结点组成。CCC的直径为2k=8，比6-立方体的6要长些。但是，CCC的结点度为3，比6-立方体的结点度6要小。在这层意义上来说，如果容许一定的时延。则CCC是一种构造可扩展系统的较好的结构。