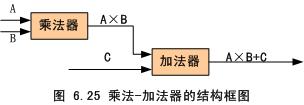
运算器输入数据的类型不同，式（6．1）的计算情况也不同。如果式（6．1）的输入是向量，输出也是向量，则计算的效率最高。这种情况下，式（6．1）可以表示为：
a［1…N］∶＝a［1…N］＋b×b［1…N］ （6．2）
　　这个等式的执行过程为：乘法器的一个输入端是标量，另一个输入端是向量Ａ，加法器的一个输入端是向量C，另一个输入是乘法器的输出，最后的输出送到为A开辟的缓冲存储区。
　　式（6．1）的另一种计算是两个输入向量通过内积运算变为一个标量。即输入两个向量和输出一个标量。这种情况下，式（6．1）可以表示为：
a∶＝a＋b［i］×c［i］ （6．3）
式（6．3）把b［i］×c［i］的乘积存入标量a中。一般的内积运算时ａ的初值为零，但使用式（6．3）的一些算法却要求ａ的初值为非零。实现式（6．3）的一个困难是两个迭代之间需要互锁，因为本次迭代的输出是下一次迭代的输入。如果加法流水线的执行时间是d个单位时间，那么两个输出之间需要互锁d-1个单位时间，以便使流水线有时间计算出变量ａ的新值供下一次迭代使用。这种方式的执行时间比式（6．2）的执行时间长d倍多。互锁使系统的效率大大降低了。
　　解决这个问题的一个方法是按式（6．4）的顺序计算式（6．3）：
ai∶＝ai-d＋bi×ci （6．4）
按这种方式计算不需要互锁，因为当ai－d出现在流水线输出端就可以被流水线输入端引用。
　　式（6．4）产生了d个不同的和，而不是式（6．3）所需的结果，还需要将这d个输出变量相加得到最后的结果。最后的求和运算需花费一小段额外时间。当向量B和B的长度较长时，求和运算的时间可以忽略不计。但是，当向量B和C的长度较短时，求和运算的时间就不能忽略了。所以当向量长度较短时，应避免采用式（6．4）所示的方法，而应采用式（6．2）所示的方法。