引起非线性流水线流水段冲突的启动距离称为禁止启动距离。如图5.13所示的非线性流水线，启动距离3都是禁止启动距离。
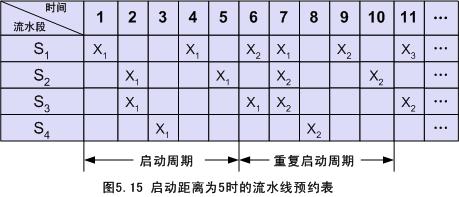
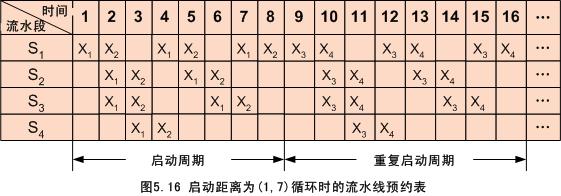
　　如图5.13的非线性流水线，当启动距离为5时的预约表如图5.15所示。从这张预约表中可以看出，任何一个流水段在任何一个时钟周期都不发生冲突。不发生冲突的启动距离不一定是一个常数，在一般情况下是一个循环数列。例如，图5.13所示的非线性流水线当启动距离为1、7、1、7、……交替循环时，任何一个流水段在任何一个时钟周期也都不发生冲突，如图5.16所示,这种使非线性流水线的任何一个流水段在任何一个时钟周期都不发生冲突的循环数列称为非线性流水线的启动循环。图5.16中的启动循环记作（1,7）。图5.15中的不发生冲突的启动距离也可以认为是一个循环数列，称为恒定循环，记作（5）。

　　要正确地调度一条非线性流水线，首先要找出流水线的所有禁止启动距离。把一条非线性流水线的所有禁止启动距离组合在一起就形成一个数列，通常把这个数列称为非线性流水线的禁止向量。
　　由预约表得到禁止向量的方法很简单，只要把预约表的每一行中任意两个"×"之间的距离都计算出来，去掉重复的，由这种数组成的一个数列就是这条非线性流水线的禁止向量。例如，对于图5.13(b)所示的预约表，第1行的第1列与第4列的两个"×"之间的距离为3，第1列与第7列的两个"×"之间的距离为6，第4列与第7列的两个"×"之间的距离也为3；第2行的第2列与第5列的两个"×"之间的距离也为3；第3行的第2列与第6列的两个"×"之间的距离为4。因此，图5.13所示非线性流水线的禁止向量为（3，4，6）。
　　把一个启动循环内的所有启动距离相加再除以这个启动循环内的启动距离个数就得到这个启动循环的平均启动距离。例如，启动循环（1，7）的平均启动距离是（1+7）/2=4。而恒定循环（5）的平均启动距离就是5。
　　非线性流水线无冲突调度的主要目标是要找出具有最小平均启动距离的启动循环，按照这样的启动循环向非线性流水线的输入端输入任务，流水线的工作速度最快，而且所有流水段在任何时间都没有冲突。下面将系统介绍非线性流水线的无冲突调度方法，这些理论最早是由E.S.Davidson及其学生们于1971年提出来的。