|
3、比较对法
比较对法实际上也是一种LRU算法。所不同的只是,它不用计数器来实现,而采用硬联逻辑实现。
LRU算法实际上要把同一组内的各个块按照被访问过的时间顺序排序,从而找出最久没有被访问过的块。一个两态的器件(触发器)能够记录两个块之间的先后顺序,多个块之间的先后顺序可以用多个两态器件的组合来实现,从而可以在多个块中找出最久没有被访问过的那个块来。
下面以三个块为例,说明比较对法的实现方法。
假设三个块分别称为块A、块B、块C,它们之间的组合共有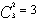 种,分别为AB、AC、BC。这些组合可以用3个两态的触发器来表示,用
种,分别为AB、AC、BC。这些组合可以用3个两态的触发器来表示,用 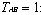 表示B块比A块更久没有被访问过,其它关系也可以用类似的方法表示。3个块之间共有6种不同的排列。它们分别表示为: 表示B块比A块更久没有被访问过,其它关系也可以用类似的方法表示。3个块之间共有6种不同的排列。它们分别表示为:
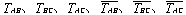 。 。
如果要表示块C最久没有被访问过,可以这样来表达:表示块C最久没有被访问过的三个块的排列顺序有两种可能,从最近到最远分别是:块A、块B、块C和块B、块A、块C。根据逻辑关系,很容易写出块C最久没有被访问过表达式:
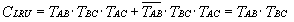
同样,也可以写出块A和块B最久没有被访问过表达式,分别为:
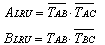
用硬件实现的逻辑图如图3.37所示。
在每次访问之后要改变比较对触发器的状态。例如,在访问块A之后,要把块A设置为最近被访问过,比较对触发器的状态应该为: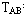 =1, =1,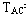 =1,触发器TBC的状态没有关系。同样,在访问块B之后,比较对触发器的状态应该为: =1,触发器TBC的状态没有关系。同样,在访问块B之后,比较对触发器的状态应该为: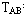 =0, =0,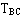 =1,触发器TAC的状态没有关系。在访问块C之后,比较对触发器的状态应该为: =1,触发器TAC的状态没有关系。在访问块C之后,比较对触发器的状态应该为: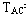 =0, =0,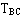 =0,触发器 =0,触发器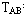 的状态没有关系。 的状态没有关系。
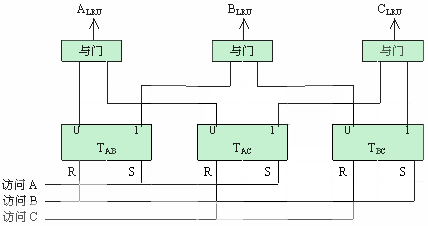 图3.37 每组3个块的比较对法
图3.37 每组3个块的比较对法
假设每组的块数为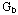 ,则需要的触发器的个数可以由下面的公式计算: ,则需要的触发器的个数可以由下面的公式计算:
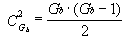
需要与门的个数为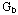 个,每个与门的输入端个数为 个,每个与门的输入端个数为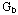 -1个。随着每组中的块数增加,所需要的触发器的个数及与门的个数成平方关系增加。表3.6给出每组不同块数情况下,所需要的触发器的个数、与门个数及与门输入端的个数。 -1个。随着每组中的块数增加,所需要的触发器的个数及与门的个数成平方关系增加。表3.6给出每组不同块数情况下,所需要的触发器的个数、与门个数及与门输入端的个数。
表3.6 每组块数与所需触发器、与门及与门输入端个数的关系
|
每组块数
|
3
|
4
|
6
|
8
|
16
|
64
|
256
|
|
触发器个数
|
3
|
6
|
15
|
28
|
120
|
2016
|
32640
|
|
与门个数
|
3
|
4
|
6
|
8
|
16
|
64
|
256
|
|
与门输入端个数
|
2
|
3
|
5
|
7
|
15
|
63
|
255
|
从表3.6中可以看出,当每组的块数为8块或8块以上时,所要的触发器个数及与门输入端个数很多,硬件实现的成本很高。这时,要采用分级的办法来实现。一般来说,所分级数越多,能节省的器件也越多,同时,器件的延迟时间也就越大。因此,采用多级方法实现的实质是用降低速度来换取节省器件。
例如,IBM 3033机的Cache每组的块数为16,分3级来实现。从第1级到第3级分别为4、2、2,它们的乘积为16块。因此,第1级要用6个触发器,第2级要用1×4=4个触发器,第3级要用1×2×4=8个触发器,总共用了18个触发器。如果不分级的话,从表3.6中看出需要触发器120个。采用分级方法节省了100多个触发器。
IBM 370/168机的Cache,采用组相联映象和变换方式。每组的块数为8,分成2级。第1级为4,第2级为2。总共需要触发器个数为:6+1×4=10个。如果不分级,则总共需要28个触发器。
由于比较对法采用的是LRU算法,因此它的块失效率比较低。另外,它的工作速度比较高,只要使用很简单的组合逻辑就能找出最久没有被访问过的块。它的主要缺点是硬件实现相对比较复杂,需要比较多的触发器,特别是当每组的块数比较大时。
|
