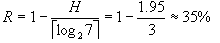2.3.2 Huffman编码法
操作码的表示方法通常有三种：固定长度操作码、Huffman编码法和扩展编码法。
一般处理机的指令条数通常为几十条至几百条，用一个字节（8位）表示，非常规整，硬件译码也很简单。IBM公司生产的许多大中型计算机，许多RISC（精简指令系统计算机）体系结构都采用这种编码方法。
固定长操作码的主要缺点是：浪费了许多信息量，即操作码的总长度增加了，从表2.4中可以看到，操作码的总长度要增加40％左右。
Huffman编码法是1992年由Huffman首先提出的一种编码方法，开始主要用于电报报文的编码。如26个英文字母中，e、t等的使用频率最高，用短码表示；q、x等的使用频率很低，用长码表示。这样，可以缩短整个报文的长度，减少报文的传送时间。Huffman编码法也可以用在其它许多地方，如存储空间压缩、时间压缩等。
要采用Huffman编码法表示操作码，必须先知道各种指令在程序中出现的概率，这通常可以通过对已有典型程序进行统计得到。
根据Huffman编码法的原理，操作码的最短长度可以通过如下公式计算：
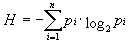
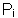表示第i种操作码在程序中出现的概率，一共有n种操作码。
如果采用固定长操作码，n种操作码共需要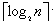 
个二进制位，因此，固定长度操作码的信息冗余量为：
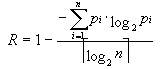
下面，我们通过一个例子来说明采用Huffman编码法来优化操作码的具体做法，并计算操作码的平均长度和信息冗余量。
假设一台模型计算机共有7种不同的操作码。如果采用固定长度操作码表示，需要3位操作码。如果采用Huffman编码法，首先要知道各种操作码在程序中出现的概率，如表2.5所示。操作码的最短长度为：
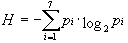
把表2.5中的数据代入上面的公式，得到操作码的最短长度：
H＝0.45×1.152＋0.30×1.737＋0.15×2.737＋0.05×4.322
＋0.03×5.059＋0.01×6.644＋0.01×6.644
＝1.95
表2.5 模型机的操作码Huffman编码法
|
指令序号
|
出现的概率
|
Huffman编码
|
操作码长度
|
|
|
0.45
|
0
|
1位
|
|
|
0.30
|
10
|
2位
|
|
|
0.15
|
110
|
3位
|
|
|
0.05
|
1110
|
4位
|
|
|
0.03
|
11110
|
5位
|
|
|
0.01
|
111110
|
6位
|
|
|
0.01
|
111111
|
6位
|
如果采用3位固定长操作码，信息的冗余量为35％。
