2.1.2 浮点数据表示

　　早期的计算机系统只有定点数据表示，这种计算机的优点是硬件结构比较简单，但有三个明显的缺点。
　　第一个缺点是编程困难，程序设计人员必须首先确定机器小数点的位置，并且把所有参与运算的数据的小数点都要对齐到这个位置上，然后机器才能正确进行运算，也就是说，编程人员首先要把参与运算的数据扩大或缩小某一个倍数后送入机器，等运算结果出来后再恢复到正确的数值。
　　第二个缺点是表示数的范围小，例如，一台16位字长的计算机所能表示的整数的范围只有：-32768到32767。从另一个角度看，为了能表示两个大小相差很大的数据，需要有很长的机器字长。例如：
　　　太阳的重量大约是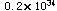： 克，
　　　一个电子的重量大约是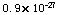：克，
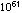　　　两者相差在以上。
　　　若用定点数据表示： ，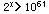
　　　解得： ｘ＞203位；
　　　再加上精度的要求，例如，要求精度不低于10进制7位，
　　　则有： ，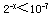
　　　解得： ｘ＞23位；
　　　总共需要： 203＋23＝230位。
　　第三个缺点是数据存储单元的利用率往往很低，例如，为了把小数点的位置确定在数据最高位之前，必须把所有参与运算的数据至少都除以这些数据中的最大数，只有这样才能把所有数据都化成纯小数，因而会造成很多数据有大量的前置零，从而浪费了许多数据存储单元。
　　为了解决上述三个问题，现代的大部分计算机都引入了浮点数据表示方式。在"汇编语言程序设计"课中，大家已经学习了浮点数的格式及其用法，在"计算机组成原理"课中，已经学习了浮点数的运算方法及运算器的工作原理等，在本书中将重点介绍浮点数据的分析和设计方法。
　　计算机中的浮点数来源于数学中的实数，但两者又有许多本质的不同，它们之间的不同见表2.1所示。

表2.1 实数与浮点数的比较

两种数据	表示数的范围	表示数的精度	唯一性
实 数	无限	连续	不冗余
浮点数	有限	不连续	冗余