二、B树的操作
（1）按关键码进行查找
假设要查找关键码等于 kval 的记录，首先将根结点读入内存进行查找，若找到，即找到了该记录所对应的物理记录位置，算法结束；否则沿着指针所指，读入相应子树根结点继续进行查找，直至找到关键码等于kval的索引项或者顺指针找到某个叶子结点，前者可由索引项取得主文件中的记录，后者说明索引文件中不存在关键码等于 kval 的记录。例如，上页图中的两条虚线表示在所示B树上查找关键码分别等于47和25的记录的过程。
（2）插入索引项
插入是在查找的基础上进行的。若在B树上找到关键码等于 kval 的索引项，则不再进行插入，否则先将关键码等于 kval 的记录插入主文件，然后将索引项插入B树。插入索引项的结点应是查找路径上最后一个非叶结点，如关键码等于25的索引项应插入在上页图所示B树的物理地址为 e 的结点中，由于 m 阶B树结点中的索引项不能超过 m-1，则当插入不能满足这个约定时，要对结点进行"分裂"操作，有时还会产生分裂连续发生直至生成新的根结点为止，如动画所示。
（3）删除索引项
删除关键码等于 kval 的记录同样也在查找的基础上进行。若在B树上没有找到关键码等于 kval 的索引项，不再进行删除操作，否则只要删除相应索引项即可。和B树的插入操作相反，在B树上删除索引项要受"结点中索引项的个数不得少于
m/2
-1"的约定，为此有时需进行"合并"结点的操作。可见在B树上进行查找是反复进行"访问外存读入结点"和"在结点中进行查找"这两个操作的过程，因此在B树上进行查找的效率取决于B树的深度，即访问外存的次数。可以证明，含N个索引项的 m 阶B树的最大深度为
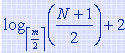；因此，在含N个索引项的 m 阶B树上进行查找访问外存的次数不超过
。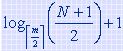