一、B树的定义
一棵"m 阶的B树"或为空树，或为具有以下特性的 m 叉查找树：
（1）树中每个结点至多有 m 棵子树；
（2）除根以外的所有非叶结点至少有
m/2
棵子树，根结点若是非叶结点，则至少有两棵子树；（3）所有的非叶结点中含有如下信息：
(n,A0,(K1,D1),A1,(K2,D2),……，An-1,(Kn,Dn),An)
其中：(Ki,Di)(i=1,…，n)为索引项，且 Ki<Ki+1(i=1,…，n-1)；
Ai(i=0,…，n) 为指向子树根结点的指针，且 Ai-1 所指子树中所有索引项的关键码小于 Ki(i=1,…，n)，An 所指子树中索引项的关键码大于 Kn，n(
m/2-1≤n≤m-1)
为结点中索引项的个数；（4）所有叶结点都在同一层上，且不含任何信息。
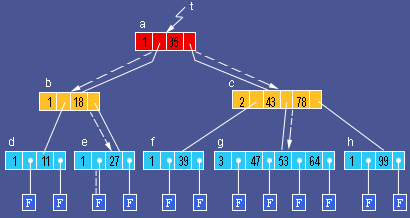
如图所示为一棵4阶的B树，其深度为4（即第4层为不带任何信息的叶子结点），图中省却了物理记录的指针 Di。
可见，和二叉查找树类似，B树也是一种查找树，其本身是一种有序结构，因此建立索引之后不需要再排序，并从下一页B树操作的叙述可见，插入或删除记录时修改索引也很方便。