二、利用"计数"和"复制"的方法实现的基数排序算法
由于在排序的过程中利用了"计数"策略,故在此称它为"计数基数排序",其算法如下所示。
void RadixSort( SqList &L )
{
// 对顺序表 L 进行基数排序
RcdType C[L.length+1]; // 开设同等大小的辅助空间用于复制数据
i= bitsnum-1;
while ( i >= 0 ) {
RadixPass( L.r, C, L.length, i );
// 对L.r进行一趟基数排序,排序结果存入 C
i--;
if (i >=0 ) {
RadixPass( C, L.r, L.length, i );
// 对C进行一趟基数排序,排序结果存入 L.r
i--;
}//if
else
for ( j=1; j<=L.length; ++j ) L.r[j] = C[j];
// 排序后的结果在C中,复制至 L.r 中
}// while
}// RadixSort
void RadixPass( RcdType A[], RcdType B[], int n, int i )
{
// 对数组 A 中记录关键字的"第i位"计数,并按计数数组
// count[] 的值将数组 A 中记录复制到数组 B 中
for ( j=0; j<RADIX; ++j ) count[j] = 0; // 计数数组初始化为0
for ( k=1; k<=n ) count[ A[k].keys[i] ] ++;
// 对关键字的对第i位"计数"
for ( j=1; j<RADIX; ++j ) count[j] = count[j-1] + count[j];
// 累加操作
for ( k=n; k>0; --k ) { // 从右端开始复制记录
j = A[k].keys[i];
B[ count[j] ] = A[k];
count[j]--;
}// for
}// RadixPass
显而易见,计数基数排序的时间复杂度为O (dn),空间复杂度为O (n)。
基数排序也可以在顺序存储结构中实现,此时的"分配"即为统计该位关键字值分别为0,1,2,…,9的记录数,"收集"即为根据统计的结果将记录复制到合适位置。
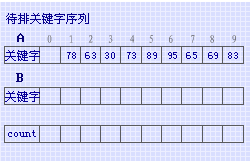
在算法中利用数组 count[] 统计并累加关键字取值从0至 k 的记录总数(k=0,1, 9),则 count[k] 即为记录序列中最后一个"关键字取值为k"的记录在每一趟的分配和收集之后在序列中的正确位置。例如,右侧示例中第一趟对"个位数"进行排序,在对个位数进行统计和累加之后,count[]={1,1,1,4,4,6,6,6,7,9},则最后一个"个位数等于3"(即关键字等于83)的记录应放在 B[count[3]] 中,同时为了确定前一个"个位数等于3"的记录应放的位置,则在将"83"复制到B[4]之后,应将 count[3] 的值"减1"。