10.5.1 2-路归并排序

　　归并排序的基本操作是将两个或两个以上的记录有序序列归并为一个有序序列。最简单的情况是，只含一个记录的序列显然是个有序序列，经过"逐趟归并"使整个序列中的有序子序列的长度逐趟增大，直至整个记录序列为有序序列止。

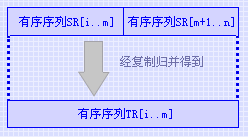
　　2-路归并排序则是归并排序中的一种最简单的情况，它的基本操作是将两个相邻的有序子序列"归并"为一个有序序列，如右侧所示。这个操作对顺序表而言是极其容易实现的，只要依关键字从小到大进行"复制"即可，如下算法所示。

算法 算法 10.15
　　void Merge (RcdType SR[], RcdType TR[], int i, int m, int n)
　{
　　// 将有序的SR[i..m]和SR[m+1..n]归并为有序的TR[i..n]
　　for (j=m+1, k=i; i<=m && j<=n; ++k)
　　{ 　　　　　　　　　// 将SR中记录按关键字从小到大地复制到TR中
　　　if (SR[i].key<=SR[j].key) TR[k] = SR[i++];
　　　else TR[k] = SR[j++];
　　}
　　while (i<=m) TR[k++] = SR[i++]; 　　// 将剩余的 SR[i..m] 复制到TR
　　while (j<=n) TR[k++] = SR[j++]; 　　// 将剩余的 SR[j..n] 复制到TR
　} // Merge

　　因此，2-路归并排序首先要得到这两个子序列，然后进行一次复制归并操作。显然产生有序子序列的简便方法即为对它们分别进行2-路归并排序，由此可得如下所示递归形式的2-路归并排序算法：
　		  

　		  
  算法 算法 10.16
　　void Msort ( RcdType SR[], RcdType TR1[], int s, int t )
　{
　　// 对SR[s..t]进行归并排序，排序后的记录存入TR1[s..t]
　　if (s==t) TR1[s] = SR[s];
　　else {
　　　m = (s+t)/2; 　　　　　// 将 SR[s..t] 平分为 SR[s..m] 和 SR[m+1..t]
　　　Msort (SR,TR2,s,m);　　// 递归地将 SR[s..m] 归并为有序的 TR2[s..m]
　　　Msort (SR,TR2,m+1, t); // 递归地将SR[m+1..t]归并为有序的TR2[m+1..t]
　　　Merge (TR2,TR1,s,m,t); // 将TR2[s..m]和TR2[m+1..t] 归并到 TR1[s..t]
　　} // else
　} // Msort
　		   　　和快速排序相类似，算法10.16是一个递归函数，因此算法中必须引入一对递归参数 s 和 t 分别表示待进行复制归并区域的上下界。在算法的递归调用过程执行中，这两个参数随着"区域的划分"而不断变化。对顺序表L进行2-路归并排序调用算法10.16时，s 和 t 的初值应分别置为1和 L.length，如算法10.17所示。

　　这是算法10.16执行过程的一个例子。动画

  
  算法 算法 10.17
　　void MergeSort (SqList &L)
　{
　　// 对顺序表L作2-路归并排序
　　MSort(L.r, L.r, 1, L.length);
　} // MergeSort

　　容易看出，2-路归并排序的时间复杂度为O (nlogn)。		   　　可如下简单分析2-路归并排序的时间复杂度：对一个长度为 n 的记录序列需进行 趟的归并，而每一趟需进行关键字比较和记录移动的时间列和 n 成正比。