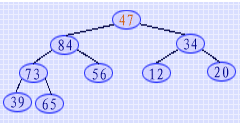
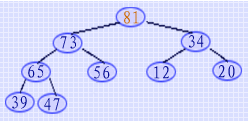
如上所述,已知关键字序列{ 98, 81, 34, 73, 56, 12, 20, 39, 65, 47 }是大顶堆,当将"98" 和"47" 互换之后,它就不再是个堆。但此时"98"已是选出的最大关键字,不需要再参加排序,由此只要对其余关键字进行排序,如果能将它重新调整为一个大顶堆,这就等于选出了第二个最大关键字。而此时的关键字序列有下列特点:如右图二叉树所示,除"根结点" 之外,其"左子树"和"右子树"都仍然是堆。由此只要 "从上到下" 进行 "筛选" 可将该序列重新调整为大顶堆。
首先将"47"移至暂存空间 R[0],将"81"和"34"进行比较后得到的"大者" 与 "47" 进行比较,由于81>47,则应将"81"移至根结点的位置,之后将"73" 和"56" 进行比较后得到的"大者"与"47" 进行比较,同样因为73>47,将"73" 上移,同理需将"65" 移至它的双亲位置,而将"47"移至它原来的位置(因为此时已达叶子结点,无孩子结点可比较)。由此得到一个新的大顶堆,选出第2个最大关键字 "81" ,之后类似地在互换"81" 和"47" 之后,进行从上到下的筛选可选出第3个最大关键字"73",依次类推直至只剩下一个关键字为止。从上到下的"筛选"算法如下所示:
void HeapAdjust (SqList &H, int s, int m)
{
// 已知H.r[s..m]中记录的关键字除H.r[s].key之外均满足堆的定义,
// 本函数依据关键字的大小对H.r[s]进行调整,使H.r[s..m]成为一
// 个大顶堆(对其中记录的关键字而言)
H.r[0] = H.r[s]; // 暂存根结点的记录
for ( j=2*s; j<=m; j*=2 ) { // 沿关键字较大的孩子结点向下筛选
if ( j<m && H.r[j].key<H.r[j+1].key )
++j; // j 为关键字较大的孩子记录的下标
if ( H.r[0].key >= H.r[j].key ) break; // 不需要调整,跳出循环
H.r[s] = H.r[j]; s = j; // 将大关键字记录往上调
}// for
H.r[s] = H.r[0]; // 回移筛选下来的记录
} // HeapAdjust
先讨论第二个问题。