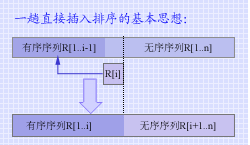
插入排序的准则是,在有序序列中插入新的记录以达到扩大有序区的长度的目的。一趟直接插入排序的基本思想则是:在对记录序列R[1..n]的排序过程中,区段R[1..i-1]中的记录已按关键字非递减的顺序排列,将 R[i] 插入到有序序列 R[1..i-1] 中,使区段 R[1..i] 中的记录按关键字非递减顺序排列,如右图所示。
由此实现一趟插入排序的步骤为:
1) 在 R[1..i-1] 中查找 R[i] 的插入位置,即确定j(0≤j<i)使得
R[1..j].key≤R[i].key<R[j+1..i-1].key
2) 将 R[j+1..i-1] 中的记录后移一个位置;
3) 将 R[i] 插入到 j+1 的位置。
和9.2.2中讨论的顺序查找类似,为了避免在查找过程中判别循环变量是否出界,设置 R[0] 为监视哨,并在查找的同时进行"记录后移",如动画演示所示。
void InsertPass( SqList &L, int i )
{
// 已知L.r[1..i-1]中的记录已按关键字非递减的顺序有序排列,本算法实
// 现将L.r[i]插入其中,并保持L.r[1..i]中记录按关键字非递减顺序有序
L.r[0] = L.r[i]; // 复制为哨兵
for ( j=i-1; L.r[0].key < L.r[j].key; --j )
L.r[j+1] = L.r[j]; // 记录后移
L.r[j+1] = L.r[0]; // 插入到正确位置
} // InsertPass
显然,只含一个记录的序列是有序的,因此令 i 从2起,逐个插入直到 n 便可实现整个插入排序,算法如下。
R[1..n] 表示记录序列的长度为 n,1..n 表示它们的序号(下标)连续地从1至 n。
void InsertSort ( SqList &L)
{
// 对顺序表L作直接插入排序
for ( i=2; i<=L.length; ++i )
if ( L.r[i].key < L.r[i-1].key ) { // 将 L.r[i] 插入有序子表
L.r[0] = L.r[i]; L.r[i]=L.r[i-1];
for ( j=i-2; L.r[0].key < L.r[j].key; --j )
L.r[j+1] = L.r[j]; // 记录后移
L.r[j+1] = L.r[0]; // 插入到正确位置
} // if
} // InsertSort