有两类处理冲突的方法。
一、开放定址法
开放定址处理冲突的办法是，设法为发生冲突的关键字"找到"哈希表中另一个尚未被记录占用的位置。
令
上式的含义是，已知哈希表的表长为 m （即哈希表中可用地址为：0～m-1），若对于某个关键字 key，哈希表中地址为 Hash(key) 的位置已被占用，则为该关键字试探 "下一个"地址
=(Hash(key)+
)
MOD m，若也已被占用，则试探再"下一个"地址 
=(Hash(key)+
)
MOD m，…，依次类推直至找到一个地址 
=(Hash(key)+
)
MOD m 未被占用为止。即 
是为解决冲突生成的一个地址序列，其值取决于设定"增量序列 
"。对于
通常可有三种设定方法：1）
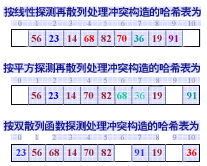
= 1,2,3,…,m-1，称这种处理冲突的方法为"线性探测再散列"。例如右侧所示哈希表，当插入关键字 23(Hash(23)=1)时，出现冲突现象，取增量
=1，求得处理冲突后的哈希地址为(1+1=)2；又如，在插入关键字36(Hash(36)=3)时，因哈希表中地址为
3,4,5 和 6 的位置均已存放记录，因此取增量 
=4，即处理冲突后的哈希地址为(3+4=)7。2）
= 12，-12，22，-22，…，±k2(k≤m/2)，称这种处理冲突的方法为"平方探测再散列"。例如右侧所示按平方探测构建的哈希表中，对于关键字68（Hash(68)=2），因表中地址为 2,3 和 1 的位置均已填入记录，因此取增量
=22，即处理冲突后的哈希地址为(3+4=)7。3）
为伪随机数列或者 =i
(key)，（(key)为关键字的另一个哈希函数），称这种处理冲突的方法为"伪随机探测再散列"或"双散列函数探测再散列"。例如右侧所示按双散列函数探测再散列构建的哈希表的增量
= i((3key)%
10+1)一个"好"的哈希函数只能尽量减少冲突，而不能避免冲突，因此如何处理发生冲突是建哈希表不可缺少的一个方面。
假设关键字序列为
{ 19,56,23,14,68,82,70,36,91 }，设哈希表的表长为11，哈希函数为 Hash(key)=key % 11
注意，开放定址法中的 
应具有"完备性"，即(1)增量序列中的各个
值均不相同；(2)由此得到的 m-1 个地址值必能覆盖哈希表中所有地址。
线性探测的增量自然满足上述要求；平方探测则只能在哈希表的表长 m 为形如 4j+3（j为整数）的素数（如：7,11,19,…等）时才能满足上述要求；双散列函数探测则要求增量哈希函数
(key)
的值和表长 m 互为素数，若 m 本身为素数，则(key)
的值可以是 1 至 m-1 之间的任何数；若表长 m 为 2 的幂次，则 (key)
的值只能取 1 和 m-1 之间任意奇数。
将所有关键字为"同义词"的记录链接在一个线性链表中。此时的哈希表以"指针数组"的形式出现，数组内各个分量存储相应哈希地址的链表的头指针。
例如，假设关键字序列为{ 19，56，23，14，68，82，70，36，91 }，哈希表的表长为 7，哈希函数为 Hash(key)=key % 7，则构建的以链地址处理冲突的哈希表如动画所示。