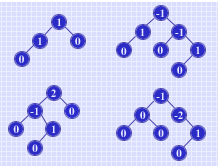
称二叉树为"平衡"指的是，它或是空树，或具有下列特性：其左子树和右子树都是平衡二叉树，且左右子树深度之差的绝对值不大于1。例如右侧上的两棵二叉树为平衡树，右侧下的两棵二叉树不是平衡树。树中结点内的数值称作结点的"平衡因子"，定义为左子树的深度减去右子树的深度。换句话说，平衡树上所有结点的平衡因子的绝对值均不大于1。可以证明，含有 n 个结点的平衡二叉树的深度为
。因此，在平衡二叉树上进行查找时，和关键字进行比较的次数是和
logn 等数量级的。"平衡"处理的原则是保证二叉查找树始终处于平衡状态。从空树起（空树是平衡树），每插入一个关键字都需要检查二叉查找树是否失去平衡，如因插入新的结点引起不平衡，则需对它进行"平衡旋转"处理。如何进行平衡旋转处理在教材和其它参考书中都有详细阐述，在此仅以一个例子作简单介绍。
假设关键字序列为{5,4,2,8,6,9}，从动画演示中可见，从空树起，依次插入5和4之后，二叉查找树仍为平衡树，但在插入2之后，它不再是平衡树。所谓"平衡旋转"处理是，在保持"查找树"的特性前提下改变结点之间的关系。例如在此时的左子树深度偏大的情况下，令左子树根为整棵树的根，而让原来的根结点成为它的右子树根。在继续插入关键字8和6之后，二叉查找树重新失去平衡，此时因为以5为根的子树为"最小不平衡子树"，故仅需对以5为根的子树进行旋转处理，但由于是因为在⑤的"右子树的左子树"上插入结点引起的不平衡，则不能简单地进行向左旋转，而是首先令⑧为⑥的左子树根（向右旋转），然后令⑤为⑥的右子树根（向左旋转）。最后由于插入关键字9使查找树失去平衡，此时以④为根的二叉树是最小不平衡子树，并且因为是在④的"右子树的右子树"上插入结点引起的不平衡，故仅需进行一次"向左旋转"处理即可。
当生成二叉查找树的关键字序列非随机时，所生成的二叉查找树有可能偏向于单支，从而使其查找性能接近于顺序表。在这种情况下，需要在生成二叉查找树的过程中进行"平衡"处理，使得在任何时刻二叉查找树的形态都是"平衡"的。
|
|||
|
你有没有看出来，为什么只需要对"最小不平衡子树"进行旋转处理？