五、查找性能分析
从二叉查找树的查找过程可见,二叉查找树的查找性能取决于它的深度,然而由于二叉查找树是在查找过程中逐个插入构成,因此它的深度取决于关键字先后插入的次序。例如,含关键字1,2,3,4,5的二叉查找树,其深度可能为3或4或5,若按1,2,3,4,5的次序得到的二叉查找树的深度为5,若按3,1,2,4,5的次序得到的二叉查找树的深度则为3,如动画所示。由此需要考察它的平均性能。
不失一般性,假设在 n 个关键字的序列中,k个关键字小于第1个关键字,n-k-1 个关键字大于第1个关键字,则由它生成的二叉查找树的左子树中含 k 个结点,右子树中含 n-k-1 个结点,其平均查找长度是 n 和 k 的函数,设为 P(n,k) 0≤k≤n-1。
假设含 n 个结点的二叉查找树的平均查找长度为 P(n),并假设生成二叉查找树是一个"随机"序列(即 k 取0至 n-1 中任一值的可能性相同),则
而在等概率查找的情况下,
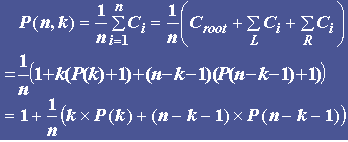
由此可得,
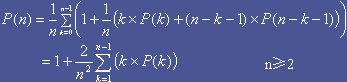
这是一个递归方程,可求得其解为:
由此可见,在随机的情况下,二叉查找树的查找性能是和 logn 等数量级的。

平均查找长度的含义即为进行一次查找所需进行 "比较"的平均次数,则 P(n) 表示在含有 n 个结点的二叉查找树上进行一次查找操作时和给定值进行比较的关键字个数,类似地,P(k) 表示在含有 k 个结点的二叉查找树上进行一次查找所需进行的关键字和给定值比较的平均次数。