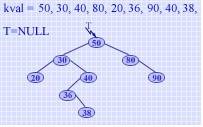
9.3.2 二叉查找树 　三、二叉查找树的插入算法 　　对于动态查找表，在查找不成功时尚需进行插入，即当二叉查找树中不存在其关键字等于给定值的结点时，需插入一个关键字定于给定值的数据元素。 　　实际上，二叉查找树结构本身正是从空树开始逐个插入生成的。插入的原则为：若二叉查找树为空树，则插入的结点为新的根结点；否则，插入的结点必为一个新的叶子结点，其插入位置由查找过程确定。例如，若给定值序列为 { 50,30,40,80,20,36,90,40,38 }，从空树起，逐个插入后构成的二叉查找树如右所示。 　　插入算法如下所示。 算法 9.6 　　bool Insert BST(BiTree &T, ElemType e ) 　{ 　　// 当二叉查找树T中不存在关键字等于 e.key 的数据元素时， 　　// 插入 e 并返回 TRUE，否则返回 FALSE 　　if (!SearchBST ( T, e.key, NULL, p ) { // 查找不成功 　　　s = new BiTNode; 　　　if (!s) exit(1);　　　　　　　　　　 // 存储分配失败 　　　s->data = e; s->lchild = s->rchild = NULL; 　　　if ( !p ) T = s; 　　　　　　　　　// 插入 *s 为新的根结点 　　　else if ( e.key < p->data.key ) 　　　　p->lchild = s;　　　　　　　　　　 // 插入 *s 为 *p 的左孩子 　　　else p->rchild = s; 　　　　　　　 // 插入 *s 为 *p 的右孩子 　　　return TRUE; 　　} // if 　　else return FALSE; 　　　// 树中已有关键字相同的结点，不再插入 　} // Insert BST

上面曾提及，由于对二叉查找树进行中序遍历得到的是一个有序序列，所以二叉查找树实质上是一个有序表。则由上述插入过程可见，可以通过生成一棵二叉查找树将一个"无序序列"变为一个"有序序列"，由此二叉查找树又称"二叉排序树"。