9.2.5 次优查找树-静态查找表的实现方法之四

算法 算法 9.3
　　void SecondOptimal(BiTree &T, ElemType R[], float sw[],
　　　　　　　　　　　　　　　　　　　　　　int low, int high)
　{
　　// 由有序表R[low..high]及其累计权值表sw(其中sw[0]==0)
　　// 递归构造次优查找树T
　　i=low; min= abs(sw[high]-sw[low]); dw = sw[high]+sw[low-1];
　　for (j=low+1; j<=high; ++j) 　　　　　　// 选择最小的ΔPi值
　　　if abs(dw-sw[j]-sw[j-1]) < min) {
　　　　i = j; min = abs(dw-sw[j]-sw[j-1]);
　　　} // if
　　T = new BiTNode;
　　T->data = R[i];　　　　　　　　　　　　// 生成根结点
　　if (i==low) T->lchild = NULL; 　　　　 // 左子树空
　　else SecondOptimal(T->lchild, R, sw, low, i-1);// 递归构造左子树
　　if (i==high) T->rchild = NULL; 　　　　 // 右子树空
　　else SecondOptimal(T->rchild, R, sw, i+1, high);// 递归构造右子树
　} // SecondOptimal

　　typedef BiTree SOSTree; 　　// 次优查找树采用二叉链表的存储结构
算法 算法 9.4
　　void CreateSOSTree(SOSTree &T, SSTable ST)
　{
　　// 由有序表ST构造一棵次优查找树T，ST的数据元素中含有权域weight
　　if (ST.length = 0) T = NULL;
　　else {
　　　FindSW(sw, ST);// 按照有序表ST中各数据元素的weight域求累计权值表sw
　　　SecondOpiamal(T, ST.elem, sw, 1, ST.length);
　　}
　} // CreateSOSTree

　　算法9.4的时间复杂度为O (nlogn)。

　　在次优查找树上进行查找的过程类似于折半查找，给定值首先和根结点的关键字进行比较，若相等，则查找成功，否则依给定值小于或大于根结点关键字继续在左子树或右子树中进行查找，直至找到和给定值相同的关键字或相应子树为空，其时间复杂度为 O(logn)。

   　
　
　　例如，已知含7个关键字的有序表及其相应的权值如下：
　　关键字　A　B　C　D　E　F　G
　　权　值　2　1　5　3　4　3　5

　　则按算法9.4和9.3构造次优查找树的过程如下所示：
动画
　

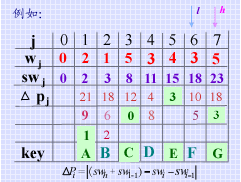
　　构造所得次优查找树以及对此有序表进行折半查找的判定树如下所示。如果将关键字的权值视作对该关键字进行的查找次数，则从两者在查找时所需进行 "给定值和关键字比较"的总次数可见，当各关键字查找概率不等时，次优查找树的查找性能优于折半查找。

　　

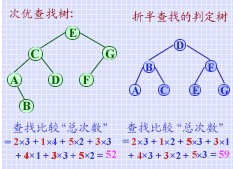
　　需要补充说明的是，由于在确定次优查找树的根结点时，仅考虑其左右子树权值和之差的绝对值为最小，而没有考察单个关键字的权值大小，因此有可能出现被选为根结点的关键字的权值较其左右相邻关键字的权值小得多，此时尚需作适当调整。

　　例如，已知7个关键字的相应权值为：
　　2,1,5,1,4,3,3，容易看出，Δ 是所有的 中的最小值，然而，w4 较 w3 和 w5 均小得多，由此，应将根结点调整为第3个关键字。由此构造所得次优查找树的PH值等于43。