在9.2.3中讨论折半查找的平均查找长度的前提是查找表中各关键字的查找概率相同。如果表中各关键字的查找概率不同，那么折半查找是否是在有序表中进行查找的最好选择呢？
例如，已知含5个关键字(A,B,C,D,E)的有序表中各关键字的查找概率依次为
=0.2,
=0.3,
=0.05,
=0.3,
=0.15，则对该有序表进行折半查找的平均查找长度为：
= 0.2
2
+ 0.33
+ 0.051
+ 0.32
+ 0.153
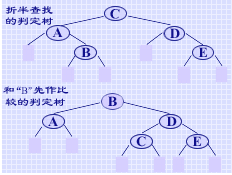
= 2.4如果改变查找时和给定值进行比较的关键字的顺序，例如对此例的有序表，令给定值首先和第二个关键字"B"进行比较，然后和关键字"A"或"D"进行比较等，其判定树如右所示。此时的平均查找长度为：
= 0.22
+ 0.31
+ 0.053
+ 0.32
+ 0.153
= 1.9显然比折半查找要好。从此例可见，当有序表中各关键字的查找概率不等时，折半查找的性能未必是最优的，那么此时的查找过程应该如何进行呢？
由于是有序表，显然希望这个查找过程仍然按"缩小区间"方式进行，只是和给定值进行比较的首选关键字不一定是位于区间中间位置的关键字，换句话说，为使平均查找长度尽可能小，应选哪一个关键字作为判定树的根结点？
如果考虑所有查找成功和查找不成功的情况，并假设每一种查找不成功的情况出现的概率为
，该定值和关键字比较的次数为
，则可定义：使得
在
以上讨论的表示静态查找表的几种结构都是线性结构，本节将介绍的一种实现方法是以"二叉树"表示静态查找表。从9.1节中的叙述读者已经知道，静态查找表的操作主要是"查询"和"检索"，很少进行插入和删除，因此一般情况下采用线性结构足矣，那么采用二叉树结构表示静态查找表的前提是什么呢？
通常称图中表示查找不成功情况的方形结点为判定树的"外结点"，反之，称表示查找成功的圆形结点为判定树的"内结点"。
容易看出，在长度为n的有序表的判定树上，有 n 个内结点和 n+1 个外结点，各个外结点恰好指示给定值小于最小关键字或大于最大关键字或介于某两个关键字之间的 n+1 种情况。
如果只考虑查找成功的情况，并为讨论方便起见引入常量 c，令
(i=1,2,…,n),(
为结点的查找概率)，则称
为结点的"权"， 称 
为带权内路径长度之和。
其中：n 为二叉树（判定树）上的结点个数(即有序表的长度)；
为第 i 个结点在二叉树上的层次。
若某个二叉树的PH值在所有具有同样权值的二叉树中近似为最小，则称它为"次优查找树"(Nearly
Search Tree)。
值和 n+1 个 
值构造最优二叉树的方法较复杂，且在 n 很大时花费的低价较高。