如果顺序表中的数据元素按关键字有序排列，即以有序表表示静态查找表时，则可进行"折半查找"。
折半查找(Binary Search)又称二分查找，其查找过程是，先确定待查记录所在范围（区间），然后逐步缩小范围直至找到该记录，或者当查找区间缩小到0也没有找到关键字等于给定值的记录为止。其算法描述如下所示：
算法 9.2int Search_Bin ( SSTable ST, KeyType kval )
{
// 在有序表ST中折半查找其关键字等于kval的数据元素，
// 若找到，则函数值为该元素在表中的位置，否则为0。
low = 1; high = ST.length; // 置区间初值
while (low <= high) {
mid = (low + high) / 2;
if ( kval == ST.elem[mid].key )
return mid; // 找到待查元素
else
if ( kval < ST.elem[mid].key )
high = mid - 1; // 继续在前半区间内进行查找
else low = mid + 1; // 继续在后半区间内进行查找
} // while
return 0; // 有序表中不存在待查元素
} // Search_Bin
例如，在有序表
(05,13,19,21,37,56,64,75,80,88,92)
中进行折半查找的过程如动画所示。
从例子可见，折半查找的过程为:给定值首先和处于待查区间"中间位置"的关键字进行比较，若相等，则查找成功，否则将查找区间缩小到"前半个区间" 或 "后半个区间" 之后继续进行查找。
log2n
+1
个关键字进行比较，显然比顺序查找要好，那么它的平均查找长度是多少呢？先看一个具体的情况，假设有序表的表长为11，则找到表中每个关键字时所需进行的给定值和关键字的比较次数如右表所列，假设表中各个关键字的查找概率相等，则在进行折半查找时的平均查找长度为：
可如下作图：将只需经过1次比较即找到的关键字（序号）放在第1层（即作为根结点），需经过2次比较找到的关键字（序号）放置在第2层，依次类推，便可得到如右所示的一棵二叉树，由于这棵二叉树描述了对长度为11的有序表进行折半查找的过程，故称之谓（对长度为11的有序表进行折半查找的）判定树。容易看出这棵判定树的深度应该和含11个元素的完全二叉树的深度相同，则对表长为 n 的有序表进行折半查找的判定树的深度和含 n 个元素的完全二叉树的深度相同，也就是说，在长度为 n 的有序表中进行折半查找，所需进行给定值和关键字的比较次数至多为
log2n+1
。假设表长 n=2h-1，则折半查找的判定树即为深度为h的满二叉树，树中第 j 层的结点数为 2j-1，并且找到和这些结点位置相应的关键字的比较次数为 j，由此，在进行等概率(折半)查找时查找成功时的平均查找长度为：
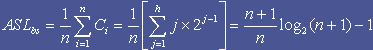
在一般情况下，可以认为有如下近似结果：
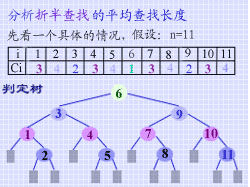
结点6表示有序表中第6个关键字。在判定树上可以一目了然地看到在折半查找的过程中，先后和给定值进行比较的关键字的位置，例如，找到表长为11的有序表中第5个关键字时，给定值先后和第6,3,4和5个关键字进行比较，换句话说，折半查找有序表中任何一个关键字恰"走了一条从根结点到该（关键字相应）结点的一条路径"。
判定树中的方形结点表示查找不成功的情况，例如，当给定值的值介于有序表中第6个和第7个关键字之间时，在给定值先后和表中第6,9和7个关键字进行比较之后，查找区间缩小到0，从判定树看，落到了⑦的左子树的位置上。
通常称表示查找成功的圆形结点为判定树的"内结点"，而称表示查找不成功的方形结点为判定树的"外结点"。