9.2.2 顺序表-静态查找表的实现方法之一

　　实现静态查找表的最简单的方法是以"顺序存储结构的线性表-顺序表"表示之。即将集合中的数据元素构成一个序列，此时的查找过程极为简单，只要从第一个或最后一个数据元素起，逐个进行"比较"直至其中某个数据元素的关键字等于给定值为止，其算法描述类似于2.2.1节中的算法2.5。

算法
　　int Search(SSTable ST, KeyType kval)
　{
　　// 在顺序表ST中查找其关键字等于给定值的数据元素，
　　// 若找到，则返回其在ST中的位序，否则返回0
　　i = 1; 　　　　　　　　// i 的初值为第1个元素的位序
　　while (i <= ST.length && (ST.elem[i].key != kval))
　　　++i; 　　　　　　　　// 依次进行判定
　　if (i <= ST.length) return i;
　　　　　　　　　　　　　　// 找到满足判定条件的数据元素为第 i 个元素
　　else return 0; 　　　// 该查找表中不存在满足判定的数据元素
　} // Search

　　可以利用留空的0号单元改写上列算法。

算法 算法 9.1
　　int Search (SSTable ST, KeyType kval)
　{
　　// 在顺序表ST中顺序查找其关键字等于 kval 的数据元素，
　　// 若找到，则函数值为该元素在表中的位置，否则为0
　　ST.elem[0].key = kval; 　　　　　　　　　　　　　// 设置"哨兵"
　　for (i=ST.length; ST.elem[i].key != kval; --i); 　// 从后往前查找
　　return i; 　　　　　　　　　　　　　　　　　　 // 找不到时，i 为0
　}　　　　　　　　　　　　　　　　　　　　　　　　// Search

　　容易看出，在顺序表中进行(顺序)查找查找成功的平均查找长度为：
　　　

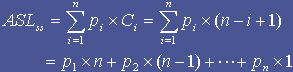
　　若查找表中每个记录的查找概率相等，即
　　　
　

   　
　
顺序表的类型描述如下：
　typedef struct
{
　ElemType *elem; // 数据元素存储空间基址，建表
　　　　　　　// 时按实际长度分配，0号单元留空
　int length; // 表中元素个数
} SSTable;

　　算法2.5中的主要操作是进行"判定(关键字的比较)"，其时间复杂度为O (ListLength(ST))。但同时为了考虑查找不成功的情况,在每次进行关键字的比较之前，首先要判断循环变量 i 是否出界，这对算法来说是必要的，但对于静态查找表查找结果是成功的情况是多余的，并且在表长大于1000的情况下，经验告诉我们，它将使查找算法的时间几乎增加一倍。

　　容易看出，在算法9.1中只是作了一点程序设计技术上的处理，利用在0号单元所设的"监视哨"控制住了循环变量 i 的出界，即在查找表中不存在其关键字等于给定值的数据元素时，i 必等于0,而这样的处理并不影响查找成功的情况。

　例如，在顺序表
　　(21,37,88,19,92,05,64,56,80,75,13)
　　中顺序查找64和60的过程如动画所示。动画		  
  　　则等概率查找时顺序查找的平均查找长度为
　　　

　　可以证明，在不等概率查找的情况下，ASLss 在 时取极小值，这就是说，如果事先已经知道查找表中各个关键字的查找概率的话，则应该按照关键字的查找概率从小而大存放数据元素。但是还有很多情况是各个数据元素的查找概率既不同，但又无法事先估计，则应该改变顺序查找的算法，令每个找到的数据元素移动到表尾位置，显然此时应该采用链式存储结构。

   　　和其它查找方法相比，顺序查找的缺点是其平均查找长度较大，特别是当表中记录数 n 很大时，查找效率较低。反之，它的优点是算法简单且适应面广，无论表中记录是否按关键字有序排列均可应用，而且，上述讨论对链式存储的线性表也同样适用。