一、求广义表的深度

　　从前述广义表的深度的定义可知，
　　　广义表的深度=Max{各个子表的深度}+1

　　由于子表亦为广义表，则可递归求解，并且空表的深度为1，若子表为原子，则其深度为0。由此可得如下算法：

算法8.1
　　int GListDepth(GList L)
　{
　　// L为指向广义表的头指针，返回L所指广义表的深度
　　if (!L) return 1; 　　　　　　　// 空表深度为1
　　if (L->tag == ATOM) return 0; 　 // 原子深度为0
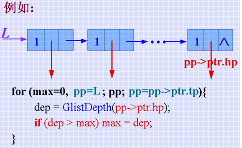
　　for (max=0, pp=L; pp; pp=pp->ptr.tp) {
　　　dep = GlistDepth(pp->ptr.hp);　 // 求以pp->ptr.hp为头指针的子表深度
　　　if (dep > max) max = dep;
　　} // for
　　return max + 1;　　　　　　// 非空表的深度是各子表的深度的最大值加1
　} // GlistDepth		  
　　从以上讨论容易看出，分治法特别适用于结构上可以分解的结构，由于广义表从结构上可以分解成 "表头 + 表尾"或者"子表1 + 子表2 +・・・+ 子表n"，因此广义表的操作通常可用分治法求解。以下列三个操作为例。

　　在设计递归算法时，关键是"调用参数的一致性" ，由于求深度的函数中的参数为指向广义表的头指针，则求子表深度的语句中的参数就应该是相应子表的头指针。

　　因此本算法的关键就是如何从已知的指针L得到各个子表的头指针。

　
　
  思考题 你有没有觉得这个算法似曾相识？它和哪个算法类似？