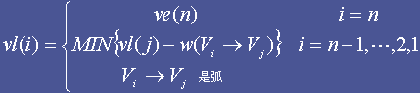| |
如何求得关键路径?首先定义四个描述量。假设顶点 为源点,Vn为汇点,事件
为源点,Vn为汇点,事件 的发生时刻为0时刻。
的发生时刻为0时刻。
ve(j):事件 可能发生的最早时刻,它是从 可能发生的最早时刻,它是从 到 到 的最长带权路径长度 的最长带权路径长度

其中,w( → → )
表示该弧的权值。对于一个特定的顶点 )
表示该弧的权值。对于一个特定的顶点 (2≤j≤n),上式表示考察 (2≤j≤n),上式表示考察 的所有前驱结点Vi1,Vi2,…,Vip,在
ve(i1)+w(Vi1→
的所有前驱结点Vi1,Vi2,…,Vip,在
ve(i1)+w(Vi1→ ),…,ve(ip)+w(Vip→ ),…,ve(ip)+w(Vip→ )
中选最大值。 )
中选最大值。
vl(i):在保证不延误整个工期(即保证Vn在ve(n)时刻发生)的前提下,事件 发生所允许的最晚时刻。它等于 ve(n) 减去
发生所允许的最晚时刻。它等于 ve(n) 减去 到 Vn 的最长带权路径长度。
到 Vn 的最长带权路径长度。
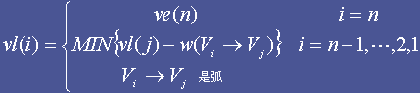
对于一个特定的顶点, (1≤i≤n-1),上式表示考察Vi的所有后继结点Vj1,Vj2,…,Vjq,在
vl(j1)-w(Vi→Vj1),…,vl(jq)-w(Vi→Vjq)
中选最小值。 (1≤i≤n-1),上式表示考察Vi的所有后继结点Vj1,Vj2,…,Vjq,在
vl(j1)-w(Vi→Vj1),…,vl(jq)-w(Vi→Vjq)
中选最小值。
ee(k):活动(令ak是 → → )可能开始的最早时刻。显然,它应该是 )可能开始的最早时刻。显然,它应该是 可能发生的最早时刻 ve(i),即
可能发生的最早时刻 ve(i),即
ee(k) = ve(i) (k=1, 2, …, m, m 为弧的数目)
el(k):活动ak(令ak
是 → → )在保证不延误整个工期的前提下,活动
ak 开始所允许的最晚时刻。不难想像,它应该是 )在保证不延误整个工期的前提下,活动
ak 开始所允许的最晚时刻。不难想像,它应该是 发生所允许的最晚时刻
vl(j) 减去 w( 发生所允许的最晚时刻
vl(j) 减去 w( → → ),即 ),即
el(k) = vl(j) - w( → → )
(k = 1, 2, …, m) )
(k = 1, 2, …, m)
由上述 ee(k) 和 el(k) 的定义可知,如果某条弧 ak
的 el(k) 和 ee(k) (1≤k≤m)值相等,则为关键活动。反之,对于非关键活动,el(k)-ee(k) 的值是该在工程的期限余量,在此范围内的延误不影响整个工程的工期,对右图所示AOE网,上述四个量的计算过程如动画所示。
| |
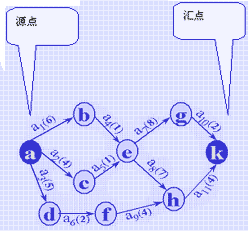
(AOE网示例) | |