若以弧表示活动，且弧上的权值表示进行该项活动所需时间，而以顶点表示"事件"，称这种有向图为活动在弧上的网络，简称活动边网络，简称为AOE(Activity On Vertex)网。所谓事件是一个关于某(几)项活动开始或完成的断言：指向它的弧表示的活动已经完成，而从它出发的弧表示的活动开始进行。因此整个有向网也表示了活动之间的优先制约关系，显然，这样的有向网中也是不允许存在有向环的，除此之外，工程的负责人还关心的是整个工程完成的最短时间以及哪些子工程将是影响整个工程如期完成的关键所在。 　　例如右图所示为表示一项假想工程的AOE网络，其中 表示第i(i=1,2,…,11)项活动，括弧内的数字表示完成该项活动所需时间（天数）。a 表示整个工程开始的事件，k 表示整个工程结束的事件，e 则表示活动a1继而a4和活动a2继而a5完成同时活动a7和a8开始进行的事件。显然表示工程开始事件的顶点的入度为零（称作源点），表示工程结束事件的顶点的出度为零（称作汇点），一个工程的AOE网应是只有一个单源点和单汇点的有向无环图。右图的AOE网将告诉人们该项工程从开始到完成需要18天，其中a1，a4，a8和a11这四项子工程必须按时开始并计划完成，否则将延误整个工程的工期，即使整个工程不能在18天内完成。称a1，a4，a8和a11为此AOE网的关键活动，称由它们构成的路径{a1,a4,a8,a11}为关键路径。 　　在AOE网络中，一条路径上各弧权值之和称为该路径的带权路径长度。由于AOE网络中某些活动可以并行进行，则完成整个工程的最短时间即为从源点到汇点最长的带权路径长度的值，这条路径便称为关键路径，构成关键路径的弧即为关键活动。

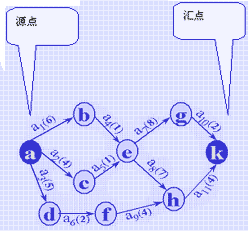
(AOE网示例)