那么如何进行拓扑排序？步骤如下： 　　（1） 在AOV网中选择一个没有前驱的顶点并输出； 　　（2） 从AOV网中删除该顶点以及从它出发的弧； 　　重复以上两步直至AOV网变空（即已输出所有顶点）或者剩余子图中不存在没有前驱的顶点。后一种情况则说明该AOV网中含有向环。 　　例如，如右所示AOV网的拓扑排序的过程如动画所示。 由于拓扑排序的结果是输出了所有的顶点，则说明该图中不存在有向环。但如果将图中从顶点 d 到顶点 e 的弧改为从顶点 e 到 d，此时图中存在一个有向环，则在拓扑排序输出顶点c之后就找不到"没有前驱"的顶点了。 　　在计算机中实现此算法时，需以"入度为零"作为"没有前驱"的量度，而"删除顶点及以它为尾的弧"的这类操作可不必真正对图的存储结构来进行，可用"弧头顶点的入度减1"的办法来替代。并且为了便于查询入度为零的顶点，在算法中可附设"栈"保存当前出现的入度为零的顶点。由此，拓扑排序的算法可如下描述： 　　建有向图的邻接表并统计各顶点的入度； 　　InitStack(S); 　　　　　　　　　// 初始化S为空栈 　　将当前所有入度为零的顶点入栈; 　　m=0; 　　　　　　　　　　　　　// 以 m 记输出的顶点个数 　　while (!StackEmpty(S)) { 　　　// 尚有入度为零的顶点存在 　　　Pop(S,v); 　　　cout<< v ; ++m; 　　　　　　// 输出入度为零的顶点，并计数 　　　w = FirstAdj(G,v);　　　　　　// w 为 v 的邻接点 　　　while (w<>0) {　　　　　　　// 将v 的所有邻接点的入度减1 　　　　inDegree[w]--; 　　　　　　// w 的入度减一 　　　　w = nextAdj(G,v,w);　　　　// 取 v 的下一个邻接点 　　　} // while w 　　} // while S 　　if (m<n) cout<<("图中有回路); // 输出的顶点数不足图中顶点数 　　DestroyStack(S);

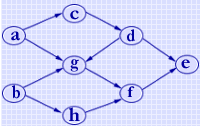
显然，拓扑有序序列中的第一个顶点应该是在整个有向图中没有任何"制约"的顶点，即没有"前驱"。在输出该顶点之后，它在拓扑有序序列中必然"领先"于所有在它之后输出的顶点，由此"删除从它出发的顶点"表示在以后的拓扑排序过程中不需要再考虑这些制约因素。 　　 　　 　 　　由于拓扑排序中对图的主要操作是"找从顶点出发的弧"，并且AOV网多数情况下是稀疏图，因此存储结构取邻接表为宜。完整算法请查阅教材《数据结构(C有"版)》第182页算法7.12 。