7.5.2 各对顶点间的最短路径问题

　　如果希望求得图中任意两个顶点之间的最短路径，显然只要依次将每个顶点设为源点，调用迪杰斯特拉算法n次便可求出，其时间复杂度为 O(n3)。弗洛伊德提出了另外一个算法，虽然其时间复杂度也是 O(n3)，但算法形式更简单。

　　弗洛伊德算法的基本思想是求得一个 n 阶方阵的序列
　　　D(-1), D(0), D(1), …,D(k),…,D(n-1)

　　其中：D(-1)[i][j] 表示从顶点 不经过其它顶点直接到达顶点 的路径长度，即
　　　D(-1)[i][j]=G.arcs[i][j]，
　　　D(k)[i][j] 则表示中间只可能经过 ,, … , 等顶点，且不可能经过 vk+1,vk+2, … ,vn-1 等顶点的最短路径长度。
　　由此，D(n-1)[i][j] 自然是从顶点 到顶点 的最短路径长度。

　　为了记下路径，和上列路径长度序列相对应有路径的方阵序列
　　　P(-1), P(0), P(1), …,P(k),…,P(n-1)

　　弗洛伊德算法的基本操作为：
　　if (D[i][k]+D[k][j] < D[i][j])
　{
　　D[i][j] = D[i][k]+D[k][j];
　　P[i][j] = P[i][k]+P[k][j]
　}

　　其中 k 表示在路径中新增添考虑的顶点号，i 为路径的起始顶点号，j 为路径的终止顶点号。
　　对有向网 G7 按弗洛伊德算法求得各对顶点之间的最短路径的过程如动画所示。动画
   　
　
　　n 为图中顶点个数，假设图中顶点依次为
　　　,,, … ,


　　换句话说，假设集合S的初始状态为空集，之后依次加入顶点,,, … 和，则 D[i][j] 表示在所有从顶点 到顶点"其中只含集合S中顶点"的路径中，路径长度的最小值。

　　　　
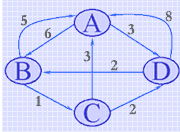
　　　　　　　　　(有向网G7)