图或网还经常用于描述一个城市或城市间的交通运输网络，以图中顶点表示一个城市或某个交通枢纽，以边或弧表示两地之间的交通状况，边或弧上的权值可表示各种相关信息，例如两地之间的路程长度，交通费用或行程时间等等。那么对于网来说，两个顶点之间的路径长度就不再是7.1节中所定义的路径中"弧的数目"，而是路径中"弧的权值之和"。则当两个顶点之间存在多条路径时，其中必然存在一条"最短路径"，即路径中弧的权值和取最小值的那条路径，本节就是讨论如何求得这条最短路径的算法。考虑到交通图的有向性，本节将讨论带权有向图(有向网)，并称路径中的第一个顶点为"源点"，路径中的最后一个顶点为"终点"。以下讨论两种最常见的路径问题。
单源点路径问题是指，已知一个有向网和网中某个源点，求得从该源点到图中其它各个顶点之间的最短路径。
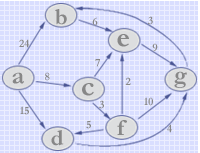
例如图 G6 中，从源点 a 到终点 b 存在多条路径，如路径 {a,b} 的长度为24，路径 {a,c,e,g,b} 的长度为27等，其中以路径 {a,d,g,b} 的长度(=22)为最短。类似地，从源点 a 到其它各顶点也都存在一条路径长度最短的路径，如右所列。
如何求得这些最短路径？迪杰斯特拉提出了一个"按各条最短路径长度递增的次序" 产生最短路径的算法。
从有向网G8的例子可见，如果从源点到某个终点存在路径，必存在一条路径长度取最小值的路径，这些最短路径彼此之间的长度不一定相等，则迪杰斯特拉算法正是按右侧所列从源点 a 到其它各终点的最短路径长度递增的次序先后产生这些最短路径。
可以如下分析这些最短路径的特点。
首先，在这些最短路径中，长度最短的这条路径上必定只有一条弧，且它的权值是从源点出发的所有弧上权的最小值。例如在图 G8 中，从源点 a 出发有3条弧，其中以弧 <a,c> 的权值为最小，由此{a,c}不仅是 a 到 c 的一条最短路径，并且它是从源点到其它各终点的最短路径中长度为最短。
其次，第二条长度次短的最短路径只可能有两种情况：它或者只含一条从源点出发的弧且弧上的权值大于已求得最短路径的那条弧的权值，但小于其它从源点出发的弧上的权值；或者是一条只经过已求得最短路径的顶点的路径，换句话说，如果第一条长度最短的最短路径是从源点 s 到
的话，若从
到 
之间存在一条弧，且路径 {s,,}
的长度比 <s,>
的权值小，则 {s,,}
是第二条长度次短的最短路径。依次类推，按迪杰斯特拉算法先后求得的每一条最短路径必定只有两种情况，或者是由源点直接到达终点，或者是只经过已经求得最短路径的顶点到达终点。
例如，求得图 G8 中从源点 a 到其它终点的最短路径的过程如右动画所示。从这个过程可见，类似于普里姆算法，在算法中应保存当前已得到的从源点到每个终点的最短路径，它的初值为：如果从源点到该点有弧，则存在一条路径，其路径长度即为该弧上的权值，之后每求得一条到达某个终点 w 的"最短路径"之后，就需要检查一下，是否存在经过这个顶点 w 的其它路径(即是否存在从顶点 w 出发到尚未求得最短路径顶点的弧)，如果存在，其长度是否比当前求得的路径长度短，如果是，则应修改当前路径。
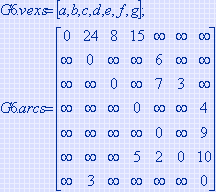
假设 n 为图 G=(V,E) 中的顶点数，dist[n] 存放从源点到每个终点当前最短路径的长度，path[n] 存放相应路径，S 为已求得最短路径的终点的集合。则迪杰斯特拉算法求最短路径的过程为：
(1) 令 S={
};
//
为源点并设定dist[i]的初始值为：
(2) 选择顶点
使得 dist[j]=Min{dist[k]|
∈V-S}，并将顶点
并入到集合S中，
(3) 对集合 V-S 中所有顶点，若存在从
指向该顶点的弧，且 dist[j]+wjk<dist[k]，则修改
dist[j] 和 path[k] 的值。
(4) 重复(2)和(3)直至求得从源点到所有其它顶点的最短路径为止。
(有向网G6)
从源点 a 到图中其它各终点的最短路径按路径长度从短到长依次为：
路径{a, c}的长度为8，
路径{a, c, f}的长度为11，
路径{a, c, f, e}的长度为13，
路径{a, d}的长度为15，
路径{a, d, g}的长度为19，
路径{a, d, g, b}的长度为22。
这应该是可以理解的，因为若它是由经过其它顶点构成的路径，那么必定不是所有最短路径中长度最短的那条。
当然，如果从v1出发有若干条弧，则<
,
>上的权值是各条弧中权值最小者。
