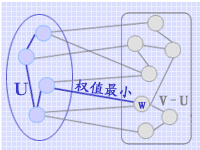
普里姆算法则从另一个角度构造连通网的最小生成树。它的基本思想是:首先选取图中任意一个顶点 v 作为生成树的根,之后继续往生成树中添加顶点 w,则在顶点 w 和顶点 v 之间必须有边,且该边上的权值应在所有和 v 相邻接的边中属最小。在一般情况下,假设图 G=(V,E) 中已落在生成树上的顶点集为U,则尚未落在生成树上的顶点集为 V-U,则从 (V-U) 顶点集中选取加入生成树的顶点 w 应满足下列条件:它和生成树上的顶点之间的边上的权值是在联接这两类顶点的所有边中权值属最小。
仍以右图所示连通网 G5 为例,假设首先选顶点 a 作为生成树的根,则此时只有顶点 a 在生成树中,其余顶点 b,c,d,e,f,g 均不在生成树上,联接这两类顶点的边只有(a,b)、(a,f) 和 (a,g),其中以边 (a,b) 的权值为最小,由此应该选择边 (a,b) 将顶点b加入到生成树中,之后链接 {a,b} 和 {c,d,e,f,g} 这两个顶点集的边除了原有的(a,f),(a,g) 之外,又增加了 (b,c) 和 (b,g),在这四条边中,权值最小的边为(b,c)(权值=8),自然应选边 (b,c),即将顶点c加入到生成树中。之后应在链接顶点集 {a,b,c} 和 {d,e,f,g} 的边集 {(a,f),(a,g),(b,g),(c,d)} 中选择权值最小的边(a,g),……,依次类推,直至所有顶点都落到生成树上为止。上述构筑生成树的过程如演示所示(过程中蓝色的边为待选边,红色的边为选中的边)。
从上述生成树的构造过程中回还可以发现一点,即每个顶点都是通过"一条边"加入到生成树上的,因此对集合 V-U 中的每个顶点,当它和集合 U 中的顶点有一条以上的边相连时,只需要保留一条权值最小的边即可。例如,当顶点 a 和 b 加入到生成树上之后,顶点 g 有两条和生成树中顶点相联接的边,由于边 (b,g) 的权值大于边 (a,g) 的权值,显然顶点 g 将来肯定不会通过边 (b,g) 加入到生成树。类似地,当顶点 g 加入到生成树之后,对顶点 f 而言,不再考虑边 (a,f)(因为它的权值比边 (g,f) 大)。由此,在普里姆算法中需要附设一个辅助数组 closedge,以记录从集合 U 到集合 V-U 中每个顶点当前的权值最小边。
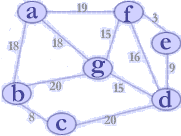
(连通网G5)
