7.3.3 深度优先生成树和广度优先生成树 　　图遍历是图的基本操作，也是一些图的应用问题求解算法的基础，以此为框架可以派生出许多应用算法。例如在遍历过程中可以求得非连通图的连通分量或强连通分量，可以利用深度优先搜索遍历求得图中两个顶点之间一条简单路径，或利用广度优先搜索遍历求得两个顶点之间的最短路径等等。在此仅以求生成树或生成森林为例说明图遍历的应用。		从以上两节中的遍历过程可见，从每个未被访问的顶点出发的深度优先搜索或广度优先搜索过程中所访问到的顶点以及所有与这些顶点相关的边构成无向图的一个连通分量，如果从第一个顶点出发的深度优先搜索或广度优先搜索即访遍图中所有顶点，则该图为连通图。 　　如果两个顶点之间存在路径，则只要从其中一个顶点出发进行深度优先搜索必能访问到另一个顶点，只是搜索路径上访问到的顶点不一定是两个顶点之间的路径上的顶点；从一个顶点出发进行广度优先搜索，一旦遇到另一个顶点求得的路径必为这两个顶点之间的最短路径，但同样的问题是需要区分搜索路径上的哪些顶点是属于这两个顶点之间的路径上的顶点。
	假设图 G=(V,E)，其中 V 是顶点的集合，E 的边(或弧)的集合。则在对图进行遍历的过程中，将边分成两个集合 T(E) 和 B(E)，其中 T(E) 中的边具有这样的特性：通过它找到 "未被访问" 的邻接点，如右图中由粗线表示的边，可称这些边为"树边"；其余的边均为集合 B(E) 中的边，可称这些边为"回边"。 　　例如，在对图 G3 进行深度优先搜索遍历过程中，从顶点 h 出发通过边找到邻接点 d，由于顶点 d 未被访问，则从 d 出发进行深度优先搜索，在对 d 进行访问之后，通过边找到邻接点 a，由于 a 已被访问，不再需要进行从 a 出发的遍历。由此 (h,d) 为树边，而 (d,a) 为回边。由深度优先搜索遍历过程中所有的树边 (T(E)) 和 n 个顶点即构成深度优先森林。例如图 G3 的深度优先森林如右所示。 　　同样，在广度优先搜索遍历的过程中，也将边集E分成树边 T(E) 和回边 B(E) 两个子集。例如右图所示为在对图 G4 进行广度优先搜索遍历过程中形成的树边(以粗线表示)和回边(以细线表示)。由广度优先搜索遍历过程中所有的树边 (T(E)) 和 n 个顶点即构成广度优先森林。例如图 G4 的广度优先森林如右所示。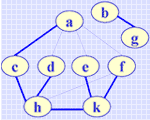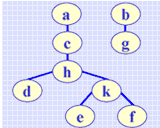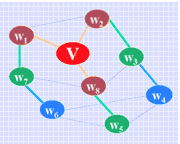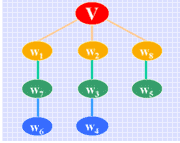		(图G3的深度优先森林) 　　 　 　　　　 　　　　　　 (图G4的广度优先森林)