二、非连通图的遍历
对于非连通图,如何确保每个顶点都能被访问到?那就只能对图中所有顶点巡查一遍"挨个检查",即从第一个顶点起,如果该顶点未被访问,则从该顶点出发进行深度优先遍历,否则接着检查下一顶点,直至所有顶点都被访问到为止。
以下是以邻接表为存储结构的深度优先搜索遍历的算法。
void DFSTraverse(ALGraph G)
{
// 对以邻接表表示的图G作深度优先遍历
bool visited[G.vexnum]; // 附设访问标识数组
for (v=0; v<G.vexnum; ++v)
visited[v] = FALSE; // 访问标识数组初始化
for (v=0; v<G.vexnum; ++v)
if (!visited[v]) DFS(G, v); // 对尚未访问的顶点调用DFS
}
例如对下列非连通图 G3 进行深度优先搜索遍历,得到顶点的访问序列为:
a→c→h→d→k→f→e→b→g
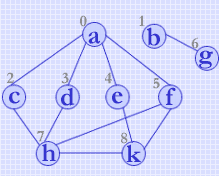
(图G3)
{
// 从第v个顶点出发递归地对图G进行深度优先搜索
VisitFunc(G.vertices[v].data); // 访问第 v 个顶点
visited[v] = TRUE; // 设访问标志
for ( p=G.vertices[ v ].firstarc; p; p=p->nextarc; )
{ // p 为指向弧结点的指针
w = p->adjvex;
if (!visited[w]) DFS(G, w);// 对v的尚未访问过的邻接顶点w递归调用DFS
} // for
} // DFS
算法7.4的时间复杂度为O(n+e)。从算法7.4可见,在遍历图时,对图中每个顶点至多调用DFS一次,因为一旦某个顶点被标识成已被访问,就不再从它出发进行搜索,而DFS过程中耗费的时间主要在于找邻接点的时间,对邻接表而言,它是
VisitFunc() 为顶点的访问函数。
对照7.2.2节中讨论的邻接表结构,可见指针 p 在第 v 个顶点的邻接点链表中移动,p 的值为空表示不存在邻接点或者没有下一个邻接点。
虽然在此以无向图为例,然而算法7.4同样适用于有向图的深度优先搜索遍历。