与二叉树和树的遍历相同，图的"遍历"是对图中的每个顶点都进行一次访问且仅进行一次访问。但由于图结构较树和二叉树更为复杂，图中任意两个顶点之间都可能存在一条弧或边，反之也可能存在某个顶点和其它顶点之间都不存在弧或边。因此对图的遍历而言，除了要确定一条搜索路径之外，还要解决两个问题：(1)如何确保每个顶点都被访问到；(2)如何确保每个顶点只被访问一次。
　		      
  　7.3.1 深度优先搜索遍历图

　一、连通图的遍历

　　从某个顶点V0出发深度优先搜索遍历连通图的定义为：
　　首先访问该顶点，然后依次从V0的各个未被访问过的邻接点出发进行深度优先搜索遍历。
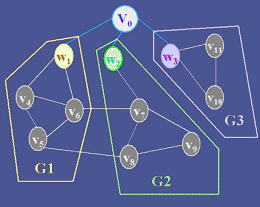
　　注意上述定义中对邻接点的"未被访问过的"修饰词语。例如下图所示的连通图 G，假设从图中顶点 V0 出发进行深度优先搜索遍历，顶点 V0 有三个邻接点 、 和 ，它们分别为 G 的三个连通子图 G1、G2 和 G3 中的一个顶点，因此在访问 V0 之后可依次从这三个邻接点出发(递归)进行深度优先搜索遍历，但由于 G1 和 G2 相互连通，则在从 出发的遍历过程中已经访问了顶点 ，由此不能再从 出发进行遍历了。

　　因此对于图的遍历，为了确保每个顶点在遍历过程中只被访问一次，需要为每个顶点建立一个"访问标志 visited[i]"，在遍历开始之前，将它们设为 "FALSE"，一旦第i个顶点被访问，则令 visited[i] 为 "TRUE"。
　

   　
　
　
　　由于二叉树和树中存在一个无前驱的"根结点"，其它所有结点都存在一条从根到该结点的路径，因此二叉树和树的遍历都只能也必须从根出发进行，而对连通图而言，图中任意两个顶点之间都有路径相通，因此可以从图中任意一个顶点出发进行遍历。

　　容易看出图的深度优先搜索遍历的过程类似于树的先根遍历。可将 V0 看作是树的根结点，、 和 可看成是它的三个"子树根结点"，如果 G1、G2 和 G3 分别为三个连通子图且相互之间不连通，则在访问 V0 之后可依次从 、 和 出发对图进行深度优先搜索遍历。
　		  
  算法7.3
　　void DFS(Graph G, int v)
　{
　　// 从顶点v出发递归地深度优先遍历图G
　　visited[v] = TRUE; VisitFunc(v); 　　　　　　// 访问顶点 v
　　for ( w=FirstAdjVex(G, v); w!=0; w=NextAdjVex(G, v, w) )
　　　if (!visited[w]) DFS(G, w);// 对v的尚未访问过的邻接顶点w递归调用DFS
　} // DFS
   　　注意这是一个伪码算法，其中参数 G 是抽象数据类型的图，v 是出发顶点的代号，w 表示是 v 的某一个邻接点，w=0 表示没有邻接点或不存在"下一个邻接点"。算法中函数 FirstAdjVex 和 NextAdjVex 的具体实现取决于图的存储结构。