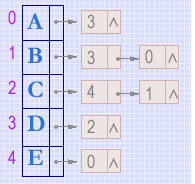
图的邻接表是应用较多的一种存储结构。从邻接表的结构定义可见,建立邻接表的主要操作是在链表中插入一个结点,以下是输入图的顶点和弧建立邻接表的算法。
void CreateGraph(ALGraph &G)
{
// 生成图G的存储结构-邻接表
cin >> G.vexnum >> G.arcnum >> G.kind;// 输入顶点数、边数和图类型
for (i=0; i<G.vexnum; ++i) { // 构造顶点数组
cin>> G.vertices[i].data; // 输入顶点
G.vertices[i].firstarc = NULL; // 初始化链表头指针为"空"
} // for
for (k=0; k<G.arcnum; ++k) { // 输入各边并构造邻接表
cin>> sv >> tv; // 输入一条弧的始点和终点
i = LocateVex(G, sv); j = LocateVex(G, tv);
// 确定sv和tv在G中位置,即顶点在G.vertices中的序号
pi = new ArcNode;
if (!pi) exit(1); // 存储分配失败
pi -> adjvex = j; // 对弧结点赋邻接点"位置"
if (G.kind==DN || G.kind==AN)
cin >> w >> p; // 输入权值和其它信息存储地址
else { w=0; p=NULL; }
pi->weight = w; pi->info = p;
pi -> nextarc = G.vertices[i].firstarc;
G.vertices[i].firstarc = pi; // 插入链表G.vertices[i]
if (G.kind==AG || G.kind==AN)
{ // 对无向图或无向网尚需建立tv的邻接点
pj = new ArcNode;
if (!pi) exit(1); // 存储分配失败
pj -> adjvex = i; // 对弧结点赋邻接点"位置"
pj -> weight = w; pj->info = p;
pj -> nextarc = G.vertices[j].firstarc;
G.vertices[j].firstarc = pj; // 插入链表G.vertices[j]
} // if
} // for
} // CreateGraph
对于一个含 n 个顶点和 e 条边的无向图,e 的最大值为 n(n-1)/2。称含有 n 个顶点和 n(n-1)/2 条边的图为完全图。如果图中边的数目 e<nlogn,则称为稀疏图,反之称为稠密图。容易理解,由于邻接矩阵的存储空间是 n2 级的,而邻接表的空间复杂度是 O (n+e)。因此通常,稠密图的存储结构取"数组表示",稀疏图的存储结构取"邻接表表示"。
按算法7.1生成的有向图G1
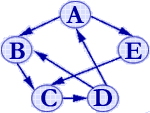
的邻接表如下所示:
有向图的邻接表中链接在每个顶点结点中的都是以该顶点为弧尾的弧,每个单链表中的弧结点的个数恰为弧尾顶点的出度,每一条弧在邻接表中只出现一次。虽然在邻接表中也能找到所有以某个顶点为弧头的弧,但必须查询整个邻接表。
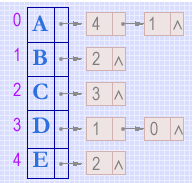
若在应用问题中主要是对以某个顶点为弧头的弧进行操作,则可以为该有向图建立一个"逆邻接表"。例如有向图G1的逆邻接表如下所示: