7.2.1 图的数组存储表示

　　假设图中顶点数为n，则邻接矩阵 定义为
　　　

　　网的邻接矩阵的定义为，当到有弧相邻接时， 的值应为该弧上的权值，否则为∞。
　　将图的顶点信息存储在一个一维数组中，并将它的邻接矩阵存储在一个二维数组中即构成图的数组表示。

图的数组(邻接矩阵)存储表示
　　const INFINITY = INT_MAX; 　　　　// 最大值∞
　　const MAX_VERTEX_NUM = 20;　　　　// 最大顶点个数
　　typedef enum {DG, DN, AG, AN} GraphKind;
　　　　　　　　　　　　　　　// 类型标志{有向图,有向网,无向图,无向网}
　　typedef struct ArcCell { 　　　　// 弧的定义
　　　VRType adj; 　　　　　　　　　　// VRType是顶点关系类型。
　　　　　　　　　// 对无权图，用1或0表示相邻否；对带权图，则为权值类型。
　　　InfoType *info; 　　　　　　　　// 该弧相关信息的指针
　　} AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
　　typedef struct { 　　　　　　　// 图的定义
　　　VertexType vexs[MAX_VERTEX_NUM]; // 顶点信息
　　　AdjMatrix arcs; 　　　　　　　　// 表示顶点之间关系的二维数组
　　　int vexnum, arcnum; 　　　　　　// 图的当前顶点数和弧(边)数
　　　GraphKind kind; 　　　　　　　　// 图的种类标志
　　} MGraph;
　		  
　　由于图结构中任意两个顶点之间都可能存在"关系"，因此无法以顺序存储映象表示这种关系，即图没有顺序存储结构。

　　图的"邻接矩阵"是以矩阵这种数学形式描述图中顶点之间的关系。
　		  
  例如，无向图G2的数组表示存储结构为：
　　　
　　　 (忽略相关信息指针)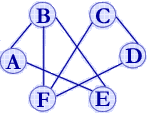
　		   　　　
　　　　　　(无向图G2)

　　容易看出，无向图的邻接矩阵为对称矩阵。每一行中"1"的个数恰为该顶点的"度"。
　
　　

  
  　　有向图G1的数组表示存储结构为：
　　　
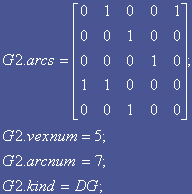　　　 (忽略相关信息指针)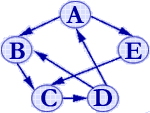 		 

　 　　　
　　　　　　　　(有向图G1)

　　有向图的邻接矩阵不一定对称。每一行中"1"的个数为该顶点的出度，反之，每一列中"1"的个数为该顶点的入度。

　　顶点的"第一个"邻接点就应该是该顶点所对应的行中值为非零元素的最小列号，其"下一个"邻接点就是同行中离它最近的值为非零元素的列号。

　　例如上列有向图中顶点A的第一个邻接点为"顶点B"(因为顶点A在顶点数组 G2.vexs 中的下标为0，又G2.arcs[0] 中非零元素的最小列下标为1，而G2.vexs[1]=B)，同样理由，顶点A相对于邻接点B的下一个邻接点是"顶点E"。