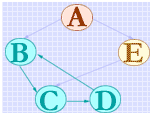
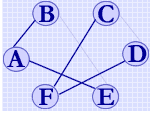
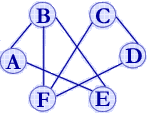
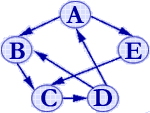
介绍几个有关图的常用术语。 　顶点的度 　　对无向图而言，邻接点的个数定义为顶点的度。例如右示无向图中顶点B的度为3，顶点C的度为2。对有向图而言，顶点的度为其出度和入度之和，其中出度定义为以该顶点为弧尾的弧的个数，入度定义为以该顶点为弧头的弧的个数。例如右示有向图中顶点D的度为3，其中出度为2，入度为1，顶点B的度为3，其中出度为1，入度为2。 　子图 　　假设有两个图 G=(V,{E}) 和 G'=(V',{E'})，如果V'V 且 E'E，则称 G'为G的子图(subgraph)。例如，右示是子图的一些例子。 　路径和回路 　　若有向图 G 中 k+1 个顶点之间都有弧存在（即<,>,<v1,>，…<,>是图 G 中的弧），则这个顶点的序列 { ,,…, } 为从顶点v0到顶点vk的一条有向路径，路径中弧的数目定义为路径长度，若序列中的顶点都不相同，则为简单路径。对无向图，相邻顶点之间存在边的 k+1 个顶点序列构成一条长度为 k 的无向路径。如果和是同一个顶点，则是一条由某个顶点出发又回到自身的路径，称这种路径为回路或环。例如右示有向图中顶点序列 {A,E,C,D} 是一条路径长度为3的简单路径，顶点序列 {A,B,C,D,A} 是一条长度为4的简单回路。右示无向图中顶点序列 {A,B,F,C,D} 是一条长度为4的无向路径。 　连通图和连通分量、强连通图和强连通分量 　　若无向图中任意两个顶点之间都存在一条无向路径，则称该无向图为连通图，否则称为非连通图。若有向图中任意两个顶点之间都存在一条有向路径，则称该有向图为强连通图。例如右上所示无向图和有向图分别为连通图和强连通图。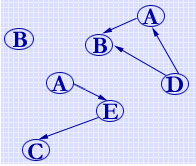 　　非连通图中各个极大连通子图称作该图的连通分量。如右图为由两个连通分量构成的非连通图。非强连通的有向图中的极大强连通子图称作有向图的强连通分量。例如右图中的有向图含有三个强连通分量。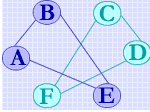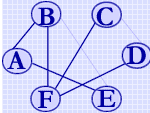 　生成树和生成森林 　　一个含 n 个顶点的连通图的生成树是该图中的一个极小连通子图，它包含图中 n 个顶点和足以构成一棵树的 n-1 条边。如右图所示。若在无向图 G2 中删除边 (B,F)，则成为一个非连通图，对于非连通图，对其每个连通分量可以构造一棵生成树，合成起来就是一个生成森林。如右图所示。 　无向网和有向网 　　在实际应用中，图的弧或边往往与具有一定意义的数相关，称这些数为"权"，分别称带权的有向图和无向图为有向网和无向网。

(无向图G2) 　　　 　　　　　　(有向图G1)