图的抽象数据类型定义如下：

ADT Graph {
　数据对象：V是具有相同特性的数据元素的集合，称为顶点集。

　数据关系：
　　VR＝{<v,w>| v,w∈V且P(v,w)，<v,w>表示从v到w的弧，
　　　　　　　　　　　　　　　　谓词P(v,w)定义了弧<v,w>的意义或信息 }

例题 例如下列定义的有向图如右图所示。
　　　G1=(V1, VR1)
　　其中：V1 = {A, B, C, D, E}
　　　VR1 ={<A,B>,<A,E>,<B,C>,<C,D>,<D,B>,<D,A>,<E,C>}

　　若<v,w>∈R 必有<w,v>∈R，则称 (v,w) 为顶点 v 和顶点 w 之间存在一条边。由顶点集和边集构成的图称作无向图。例如下列定义的无向图如右所示。
　　　G2=(V2, VR2)其中：V2={A, B, C, D, E, F}
　　　VR2={(A,B),(A,E),(B,E),(C,D),(D,F),(B,F),(C,F) }

  
　图由一个顶点集和弧集构成，通常写作：
　　Graph=(V,VR)。由于空的图在实际应用中没有意义，因此一般不讨论空的图，即V是顶点的有穷非空集合。

　　<v,w>表示从顶点 v 到顶点 w 的一条弧，其中顶点 v 被称为弧尾，顶点 w 被称作弧头。由于弧是有方向的，故称有向图。

　　　　
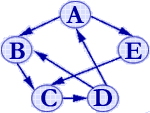
　　　　　　　(有向图G1)

　　　　
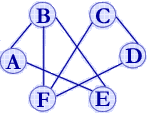
　　　　　　　(无向图G2)