【基础知识题】
1. 已知一棵树边的集合为{<I,M>,<I,N>,<E,I>,<B,E>,<B,D>,<A,B>,<G,J>, <G,K>,<C,G>,<C,F>,<H,L>,<C,H>,<A,C> },请画出这棵树,并回答下列问题:
(1) 哪个是根结点?
(2) 哪些是叶子结点?
(3) 哪个是结点 G 的双亲?
(4) 哪些是结点 G 的祖先?
(5) 哪些是结点 G 的孩子?
(6) 哪些是结点E的子孙?
(7) 哪些是结点 E 的兄弟?哪些是结点F的兄弟?
(8) 结点 B 和 N 的层次号分别是什么 ?
(9) 树的深度是多少?
(10) 以结点 C 为根的子树的深度是多少?
2. 一棵度为 2 的树与一棵二叉树有何区别?
3. 试分别画出具有 3 个结点的树和 3 个结点的二叉树的所有不同形态。
4. 已知在一棵含有 n 个结点的树中,只有度为 k 的分支结点和度为 0 的叶子结点。试求该树含有的叶子结点的数目。
5. 试分别推导含 n 个结点和含 n0 个叶子结点的完全三叉树的深度 H。
6. 假设 n 和 m 为二叉树中两结点,用“1”、“0”或“ф”(分别表示肯定、恰恰相反或者不一定)填写下表:

注:如果(1)离 a 和 b 最近的共同祖先 p 存在,且(2)a 在 p 的左子树中,b 在 p 的右子树中,则称 a 在 b 的左方(即 b 在 a 的右方)。
7. 找出所有满足下列条件的二叉树:
(a) 它们在先序遍历和中序遍历时,得到的结点访问序列相同;
(b) 它们在后序遍历和中序遍历时,得到的结点访问序列相同;
(c) 它们在先序遍历和后序遍历时,得到的结点访问序列相同;
8. 将下列二叉链表改为先序线索链表。

9.
阅读下列算法,若有错,则改正之。
BiTree InSucc( BiTree q ) {
//
已知 q 是指向中序线索二叉树上某个结点的指针,
//
本函数返回指向 *q 的后继的指针。
r = q->rchild;
if ( !r->rtag
)
while ( !r->rtag ) r = r->rchild;
return
r;
} //InSucc
【基础知识题】
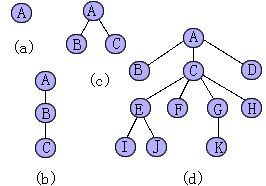
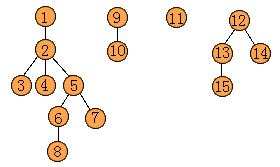
12. 对于 10 题中给出的各树分别求出以下遍历序列:
(1) 先根序列; (2) 后根序列。
13. 假设用于通讯的电文仅由 8 个字母组成,字母在电文中出现的频率分别为 0.07, 0.19, 0.02, 0.06, 0.32, 0.03, 0.21, 0.10。试为这 8 个字母设计哈夫曼编码。使用 0~7 的二进制表示形式是令一种编码方案。对于上述实例,比较两种方案的优缺点。
14. 假设一棵二叉树的前序序列为 EBADCFHGIKJ 和中序序列为 ABCDEFGHIJK。请画出该树。
15. 假设一棵二叉树的中序序列为 DCBGEAHFIJK 和后序序列为 DCEGBFHKJIA。请画出该树。