赫夫曼二叉树在通讯编码中的一个应用是利用它构造一组最优前缀编码。在某些通讯场合,需将传送的文字转换成由二进制字符组成的字符串。
通常有两类二进制编码:一类为等长编码,这类编码的二进制串的长度取决于电文中不同的字符个数,假设需传送的电文中只有四种字符,只需两位字符的串便可分辨,但如果电文中可能出现26种不同字符,则等长编码串的长度为5。另一类是不等长编码,即各个字符的编码长度不等。
不等长编码的好处是,可以使传送电文的字符串的总长度尽可能地短。因为通常各个字符在电文中出现的次数是不相同的,若对出现次数较多的字符采用尽可能短的编码,则传送电文的总长便可减少。但在实用的不等长编码中,任意一个字符的编码都不能是另一个字符的编码的前缀,这种编码称为前缀编码。
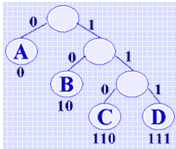
可以利用二叉树来设计二进制的前缀编码。假设有一棵如右图所示的二叉树,其四个叶子结点分别表示A、B、C和D四个字符,且约定左分支表示字符'0',右分支表示字符'1',则以由从根到叶子的路径上的分支表示的字符组成的字符串作为该叶子结点字符的编码。如右图中A、B、C和D的二进制前缀编码分别为0、10、110和111。容易证明,如此得到的必为二进制前缀编码。并且,若以字符出现的次数为权,构造一棵赫夫曼树,由此得到的二进制前缀编码便为"最优前缀编码"(赫夫曼编码)。即以这组编码传送电文可使电文总长最短(对所有其它前缀编码而言)。
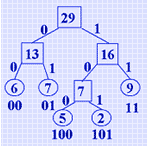
假设电文总只有5个字符,且在电文中出现的频率分别为:
5/29,6/29,2/29,9/29,7/29。则所构造的最优前缀编码如右图所示。
例如,假设需传送的电文为"ABACCDA",它只有A、B、C和D四种字符,可设它们的编码分别为00、01 、10和11,则上述七个字符的电文便为 "000100101100",总长14位。显然这样的等长编码便于译码,对方接收时,可按两位一分进行译码。
例如根据上述电文中的四个字符A、B、C和D在电文中出现的多少为它们设计的编码分别为0、00、1和01,则上述七个字符的电文可转换成总长为9的字符串"000011010"。但是,这样的编码产生一个新的问题,即如何反译成原文,除非在每个字符之间加上空格符,否则将产生多义性。例如上述字符串中前四个字符的子串"0000"就可有多种译法,或"AAAA",或是"ABA",也可以是"BB"等。