最优树，又称赫夫曼树（Huffman Tree）是一类带权路径长度最短的树，本节仅限于讨论最优二叉树。
首先介绍路径和路径长度的概念。由从树的根结点到其余结点的分支构成一条路径，路径上的分支数目称路径长度。一般情况下，树的路径长度指的是从树根到树中其余每个结点的路径长度之和。6.2.2节中定义的完全二叉树就是这种路径长度最短的二叉树。
结点的带权路径长度则定义为从树根到该结点之间的路径长度与该结点上所带权值的乘积。假设树上有 n 个叶子结点，且每个叶子结点上带有权值为
(k=1,2,…,n)，则树的带权路径长度定义为树中所有叶子结点的带权路径长度之和，通常记作
其中
为带权
的叶子结点的带权路径长度。假设有 n 个权值{
，
，…
}，试构造一棵有
n 个叶子结点的二叉树，每个叶子结点带权为
。显然，这样的二叉树可以构造出多棵，其中必存在一棵带权路径长度
WPL 取最小的二叉树，称该二叉树为最优二叉树。最优树并不特指二叉树，但"带权路径长度最短 "是在"度相同"的树中比较而得的结果，因此有最优二叉树、最优三叉树之称等等。
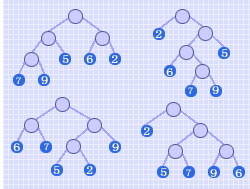
例如，右图中的四棵二叉树，都有5个叶子结点且带相同权值5、6、2、9、7，它们的带权路径长度分别为WPL = 7
3 + 9
3 + 5
2 + 6
2 + 2
2 = 74 (左上图)WPL = 2
1 + 6
3 + 7
4 + 9
4 + 5
2 = 94 (右上图)WPL = 6
2 + 7
2 + 5
3 + 2
3 + 9
2 = 65 (左下图)WPL = 2
1 + 5
3 + 7
3 + 9
3 + 6
3 = 83 (右下图)其中以左下图中二叉树的带权路径长度为最小。可以验证，它恰为最优二叉树，即在所有叶子结点带权为5、6、2、9、7的二叉树中，带权路径长度的最小值为65。
