三、构建树的孩子-兄弟链表存储结构
和构建二叉树的存储结构相同,构建树的存储结构的算法也取决于输入的形式。
假设在输入根结点之后,以(双亲、孩子)的形式输入树中各个分支的有序对,并且各分支的输入次序为自上而下,同层次则为从左到右。例如,对右图所示树的分支先后输入的次序为:(A,B),(A,C),(A,D),(B,E),(D,F),(D,G),(E,H),(E,I),(E,J),(G,K)。
这个输入次序决定了这个建存储结构的算法为"按层次遍历",即按输入的次序自上而下、自左至右建立"孩子"结点,同时查询双亲的位置,建立和双亲结点的关系。
由于按层次遍历的规则是:"其父结点先被访问的孩子结点"先于"其父结点后被访问的孩子结点"进行访问,因此在按层次遍历的算法中需要一个"队列"用以记录父结点被访问的先后次序,以便按此次序先后访问他们的孩子结点。
void CreateTree( CSTree &T )
{
// 按自上而下且每一层自左至右的次序输入双亲-孩子的有序
// 对,建立树的孩子-兄弟链表,T为指向根结点的指针
Queue Q;
cin >> n; // 输入树的结点数
if (n==0) T=NULL;
else {
InitQueue(Q); // 初始化空队列
T = new CSNode;
if (!T) exit(1); // 存储分配失败
cin >> T->data; // 输入树的根结点元素
T->firstchild = T->nextsibling = NULL;
EnQueue(Q, T); // 根结点入队列
for (k=1; k<n; k++) {
cin >> fa >> ch; // 输入一个分支
s= new CSNode; // 建孩子结点
if (!s) exit(1); // 存储分配失败
s->data = ch; s->firstchild = s->nextsibling = NULL;
GetHead(Q, p);
while (p->data != fa) { // 查询双亲结点
DeQueue(Q, p); GetHead(Q, p);
} // while
if (!p->firstchild) // 当前输入的是第一个孩子
{ p->firstchild = s; r = s; }
else { p->nextsibling = s; r = s; }
EnQueue(Q, s); // 新建的孩子结点入队列
} // for
DestroyQueue(Q);
} // else
} // CreateTree
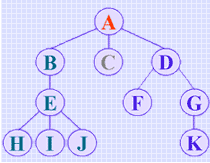
例如,在建立根结点A的同时将该结点的"指针" 入队列,在依次输入(A,B),(A,C),(A,D)时可由队头元素找到父结点的位置,同时在继续输入(B,E)时,因为当时的队头元素中的指针所指结点不是双亲B,可判断出A的孩子结点已都输入完毕,即不再需要保留结点A的指针。换句话说,为了找到结点B的指针应该将队列元素出列直至队头元素的指针指向当前输入的双亲结点为止。
例如,在先后输入下列数据
11,A,(A,B),(A,C),(A,D),(B,E),(D,F)
建立孩子-兄弟链表过程中队列状态的变化情况如动画所示。