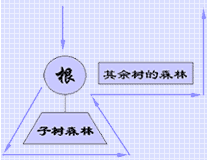
森林是树的集合,由此可以对森林中的每一棵树依次从左到右(如右图所示)进行先根遍历或者后根遍历。又森林中的(第一棵树的根)、(第一棵树的子树森林)及(其余树构成的森林),分别对应为(二叉树的根)、(二叉树的左子树)和(二叉树的右子树)。由此可如下定义森林的这两种遍历。
一、先序遍历森林
若森林不空,则可依下列次序进行遍历
(1) 访问森林中第一棵树的根结点;
(2) 先序遍历第一棵树中的子树森林;
(3) 先序遍历除去第一棵树之后剩余的树构成的森林。
二、中序遍历森林
若森林不空,则可依下列次序进行遍历:
(1) 中序遍历第一棵树中的子树森林;
(2) 访问森林中第一棵树的根结点;
(3) 中序遍历除去第一棵树之后剩余的树构成的森林。
容易看出,树的先根遍历即森林的先序遍历可对应到二叉树的先序遍历,树的后根遍历即森林的中序遍历可对应到二叉树的中序遍历。换句话说,若以孩子-兄弟链表作树(或森林)的存储结构,则树的先根遍历(或森林的先序遍历)的算法和二叉树的先序遍历算法类似,而树的后根遍历(或森林的中序遍历)的算法和二叉树的中序遍历算法类似。