如何在中序线索链表上进行遍历,关键问题有二:
一是如何找到访问的第一个结点?
二是如何找到每个结点在中序序列中的后继?
首先,在中序线索链表上如何找到中序序列中的第一个结点?
根据6.4.1节中对二叉树的中序遍历的定义可知,中序遍历访问的第一个结点必定是 "其左子树为空"的结点。若根结点没有左子树,则根结点即为中序遍历访问的第一个结点,若根结点的左子树不空,则访问的第一个结点应该是其左子树中"最左下的结点",即从根结点出发,顺指针 Lchild 找到其左子树直至某个结点的指针 Lchild 为"线索"止,该结点必为中序序列中的第一个结点。如右图所示例子中的"结点D"。
如何在中序线索链表中找结点的后继?
若结点没有右子树,即结点的右指针类型标志 Rtag 为"Thread",则指针 Rchild 所指即为它的后继,如右图所示例子中的"结点D"、"结点G"等,若结点有右子树,则它的后继应该是其右子树中访问的第一个结点。和前面所述找二叉树的第一个结点一样,就应该从它的右子树根出发,顺指针 Lcuild 直至没有左子树的结点为止,该结点即为它的后继。例如右图中结点B的后继为结点G。
void InOrderTraverse_Thr(BiThrTree Thead,void (*Visit)(ElemType e))
{
// Thead 指向中序线索链表中的头结点,头结点的左指针 Lchild
// 指向二叉树的根结点,头结点的右线索 Rchild 指向中序遍历
// 访问的最后一个结点。本算法对此二叉树进行中序遍历,对
// 树中每个数据元素调用函数 Visit 进行访问操作
p = Thead->Lchild; // p 指向二叉树的根结点
while (p!= Thead) { // 空树或遍历结束时,p==Thead
while (p->LTag==Link) p = p->Lchild;
Visit(p->data); // 访问其左子树为空的结点
while (p->RTag==Thread && p->Rchild!=Thread) {
p = p->rchild; Visit(p->data); // 访问"右线索"所指后继结点
} // while
p = p->Rchild; // p 进至其右子树根
} // while
} // InOrderTraverse_Thr
以线索链表作存储结构,即以指向线索链表中头结点的指针表示二叉树。由于在线索链表中已经包含有遍历得到的访问次序序列的信息,则在线索链表中进行遍历可以递推进行。即首先找到遍历中应该访问的"第一个"结点,而后接着顺每个结点的"后继"依次进行访问。在此仅以中序线索链表为例进行讨论。
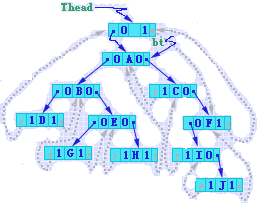
因为结点B的 RTag=Link,则顺指针 Rchild 找到它的右子树根(结点E),因为结点E的 LTag=Link,则顺指针 Lchild 找到它的左子树根(结点G),而因为结点 G 的 Ltag=Thread,说明G是结点B的右子树中"最左下" 的结点,所以结点G是结点B的后继。
读者可以观看对上图的中序线索链表进行遍历的过程加深对算法6.9的理解。![]()
可见,在线索化链表上进行遍历省去了递归栈。
其它序线索链表的遍历算法也类似,关键在于找后继结点,只是在后序线索链表上找后继还需要知悉结点"双亲"的的位置。